СПбГИКиТ стал правообладателем программы для ЭВМ в области фундаментальных научных исследований

В научном проекте кафедры аудиовизуальных систем и технологий СПбГИКиТ, посвященном фундаментальным исследованиям в термодинамике и молекулярно-кинетической теории рассматриваются методологические аспекты реализации модели научного исследования в системе технического образования. Основой создания теории физического явления является феноменологический подход, создающий общую картину явления и устанавливающий основные фундаментальные соотношения без подробной детализации модельных представлений, на основе использования фундаментальных научных законов и надежно установленных экспериментальных данных.  

Комплекс программ «Анимационная модель вращательного броуновского движения» завершает цикл научных исследований кафедры аудиовизуальных систем и технологий в области современной методологии стохастического моделирования реальных процессов и систем.

В ходе научных исследований вращательной броуновской динамики:

• проведены исследования в теории чисел, приведены компьютерные иллюстрации гипотетического нормального свойства фундаментальных констант в десятичной и двоичной системе счисления;
• разработан табличный генератор псевдослучайных чисел с равномерным распределением (π-генератор), проведен статистический тест программы. Получен явный вид плотности распределения χ²-критерия и графическая интерпретация статистического критерия в системе компьютерной алгебры Maple;
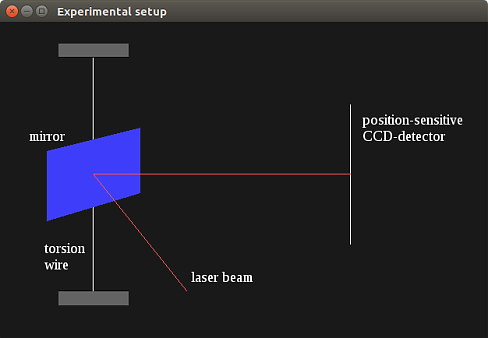
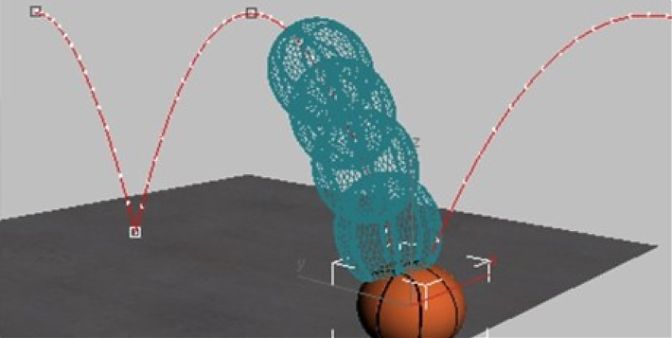
• разработана компьютерная модель случайных блужданий в поступательном броуновском движении, а также анимационная модель исторического опыта Капплера во вращательной броуновской динамике в рамках вероятностно-статистического подхода с  использованием π-генератора псевдослучайных чисел, классической плотности вероятности осциллятора и функций системы символьной математики.

Для разработки анимационной модели определены критерии выбора компьютерной среды, языка программирования и библиотек:

• возможность реализации модели на выбранном уровне детализации;
• простота освоения доступных команд библиотек языка и компиляции полученного кода;
• материальная доступность, наличие бесплатной лицензии на программное обеспечение;
• опыт работы исследователя в выбранной среде, уровень знакомства с синтаксисом языка, парадигмами программирования и доступными библиотеками;
• способность работы языка на платформах Windows и Linux (кроссплатформенность).

Высокий уровень языка Python  помогает быстро осваивать его особенности и не заботиться о множественных сложностях языков низкого уровня. Широкое распространение языка предоставляет возможность выбирать инструменты построения графики и анимации из множества доступных библиотек. Библиотека PyPI (The Python Package Index) содержит более сотни тысяч различных проектов. Широкое сообщество пользователей позволяет получить поддержку при возможном возникновении проблем. Свободная лицензия Python Software Foundation License позволяет использовать язык без каких-либо ограничений. Кроссплатформенность позволяет разрабатывать приложения в операционной системе Linux с рабочего ноутбука, при необходимости имея возможность перейти на другую известную платформу.

  Скриншот программы анимационного моделирования вращательного броуновского движения

Для визуализации опыта используется набор инструментов для графики и анимации. Стандартом для платформонезависимой прорисовки графики является OpenGL – спецификация двух- и трёхмерной графики. OpenGL также не зависит от языка программирования и имеет привязки к множеству из них, в том числе к Python. Одной из python-библиотек, работающих с OpenGL, является Pyglet. Pyglet позволяет рисовать OpenGL примитивы, работать с окном, управлять временем для создания анимации, загружать мультимедиа-объекты.

Разработанная компьютерная программа используется для исследования дифференциальных уравнений динамической модели вращательного броуновского движения, в которой рассматриваются малые колебания в окрестности положения равновесия крутильного маятника.

Перспективы практического использования программы «Анимационная модель вращательного броуновского движения», правообладателем которой является СПбГИКиТ, связаны с актуальными проблемами проектирования интеллектуальных систем математического моделирования реальных процессов и систем, а также с методикой их изучения. Полученные результаты применимы в новых методических разработках в области моделирования и формализации, специальность 05.13.18- Математическое моделирование, численные методы и комплексы программ, а также в образовательных программах направлений подготовки 11.03.01- Радиотехника, 44.03.01- Педагогическое образование, модуль- Информатика, информационные технологии и вычислительная физика, 09.03.02- Информационные системы и технологии.

Публикации по теме исследования:

1. Ходанович А.И. Компьютерные иллюстрации математических гипотез в интерактивной графике. Эл. научный журнал «Современные проблемы науки и образования». – 2015. – № 5; URL:  www.science-education.ru/128-21941   (в соавт.)
2. Khodanovich A. The physical and mathematical education in the context of modern metodology of scince. International Conference “Scientific research of the SCO countries: synergy and interration”, Beijing, China, PRC, 2018, P 244-148.
3. Ходанович А.И. Вероятностно-статистические методы и модели в учебном компьютерном эксперименте. Международный научный журнал «Мир науки, культуры, образования», № 1(62), 2017.- С 210-214. (в соавт.)
4. Ходанович А.И. Современные информационные технологии в технических проектах СПбГИКиТ. Инновационные технологии в медиаобразовании: материалы II Международной научно-практической конференции, 29, 30 мая 2017 г. / редкол. : А. И. Ходанович (отв. ред.) [и др.]. – СПб. : СПбГИКиТ, 2018. – С 242-250. (в соавт.)
5. Ходанович А.И. Методологические аспекты стохастического моделирования в медиаобразовании. Инновационные технологии в медиаобразовании. Материалы III Международной научно-практической конференции, 4,5 окт. 2018 г.- СПб.: СПбГИКиТ, 2019.- С 13-21.

Кафедра аудиовизуальных систем и технологий