Проекты
Межвузовский научный творческий проект
«КИНО В НАУКЕ: ВЗГЛЯД НА НАУЧНЫЙ МЕТОД ЧЕРЕЗ ОБЪЕКТИВ КИНОКАМЕРЫ»

Аннотация
В проекте рассматриваются особенности методологического и компетентностного подхода в системе кинообразования, профессиональной подготовке инженеров и технических специалистов в киноиндустрии. Приведены примеры прикладных задач с видеоконтентом в области математического и компьютерного моделирования. Подробно рассматривается методика решения физических и технических задач с реальными объектами и неполными данными, потому что именно с такими, а отнюдь не идеализированными объектами придётся иметь дело будущему инженеру в своей профессиональной деятельности. Рассматриваются различные подходы к работе с изображением в кадре. В статье указаны подходы к составлению физических моделей, адекватным реальным физическим объектам, получению математических моделей и их решению. Описана работа с видеоконтентом на примере реального видео с видеохостинга YouTube. Приведены примеры оценки масштабов изображения в кадре и выявления условий, заданных неявно, с использованием дополнительных источников информации. Разработанная методика использования задач с видеоконтентом позволит решить проблему создания медиатеки, необходимой для формирования профессиональных компетенций современного киноинженера. Приведены примеры использования техники и методологии кинематографа в научных исследованиях. Полученные практические результаты могут быть применены в новых научных и методических разработках в области медиаобразования.
Актуальность и новизна научного исследования
Современный методологический подход к кинообразованию носит практико-ориентированный характер, подготовка будущего инженера в сфере кинематографии требует умения решать широкий спектр прикладных задач, умения работать и с реальными объектами, и с моделями или макетами в условиях киносъемки. Переход от реальных объектов к физическим моделям требует специфических навыков, таких как системное мышление, «умение видеть за деревьями лес и за лесом деревья» - умение одновременно представлять объект как единое целое и в деталях, понимание поведения объекта целиком и взаимодействия его составляющих, умение идеализировать объект, выделяя его существенные свойства и абстрагируясь от несущественных... Научный метод перехода от объекта к модели всегда требует значительного числа допущений и упрощений. Чтобы научиться грамотно составлять физические модели студенты должны уметь выбирать главные, наиболее подходящие для цели исследования свойства реального объекта, делать грамотные оценки свойств объектов, пользоваться дополнительными источниками информации. Методологией научного проекта является компетентностный подход в медиаобразовании, задачный подход в теории и методике обучения физике, методы демонстрационных примеров, методы учебного физического эксперимента, а также феноменологический подход в моделировании реальных процессов и систем с использованием информационных и коммуникационных технологий. В работе использовалась учебная медиатека, современная видеоаппаратура кино и телевидения.
Библиографический этап научного творческого проекта
В теоретической подготовке киноинженера необходимо отметить иерархию законов, в которой важные в прикладных задачах законы сохранения следуют из той или иной симметрии пространства-времени. Симметрия пространства и времени неразрывно связана с фундаментальными законами сохранения: закон сохранения энергии вытекает из однородности времени, закон сохранения импульса следует из однородности пространства, закон сохранения момента импульса выводится из изотропности пространства.
Данная связь для консервативных систем выводится из теоремы, доказанной Эмми Нётер в 1918 году. Теорема Нётер показала природу законов сохранения, связанную с инвариантностью уравнений движения при тех или иных преобразованиях координат и времени. К таким преобразованиям относится так называемое масштабное преобразование, при котором координаты и время увеличиваются или уменьшаются в определенное число раз:  , где α, β – некоторые масштабные множители. Очевидно, что при постоянной массе кинетическая энергия преобразуется
, где α, β – некоторые масштабные множители. Очевидно, что при постоянной массе кинетическая энергия преобразуется  [1, с.205].
[1, с.205].
Преобразование потенциальной и полной энергии зависит от координат и позволяет находить связь пространственных и временных характеристик движения без обращения к законам динамики, потому что преобразование энергии можно рассматривать при изменении самой физической системы, считая единицы измерения прежними. Наивысшим проявлением симметрии пространства-времени является принцип относительности - эквивалентность инерциальных систем отсчета. Переход между уровнями методологических принципов, законов сохранения и частных законов и теорий показывает уровень нашего понимания окружающего мира.
Заметим, что в методике решения задач учет симметрии и масштабные преобразования существенно упрощают алгоритм, основанный на «принципе относительности» для актуальных задач кинематографа. В данном случае рассматривается реальная сцена (система координат K(r,t))) и экран воспроизведения видеофильма (система координат K'(r',t'))), т.е. «инерциальные системы отсчета». Возможна постановка двух типов задач. Первая задача: по известному времени съемки и времени воспроизведения видеоконтента определение частоты кадров. Вторая задача: по известным параметрам изображения на экране и частоте съемки восстановление параметров сцены, например, траектории движения тела [7].

Рис. 1. Симметрия при масштабных преобразованиях кадра [2],[7]
Методологический этап творческого проекта (2024 г.).
Компьютерная анимация динамических моделей в современной физической электронике: история и перспектива научных исследований
С распространением компьютерных технологий появилась компьютерная анимация, применение которой не ограничивается только сферой искусства: она востребована на производстве и в науке при проектировании машин и сооружений, моделировании процессов, в деловой и торговой сферах. Компьютерная анимация, как и компьютерная графика, использует векторную, растровую, фрактальную и трёхмерную графику (3D) для ввода, отображения и преобразования графических объектов, и методы постоянно развиваются вслед за развитием IT-технологий. Компьютерной называют анимацию изображений на экране монитора, синтез динамических изображений на компьютере, визуализация моделей с физической симметрией и применением специальных компьютерных программ, создающих анимацию, и форматов графических файлов, поддерживающих её воспроизведение.

Компьютерная анимация, как методология кинематографа приобретает особое значение в фундаментальных научных исследованиях и их популяризации на основе современной интерактивной графики, системы символьной математики и численного анализа. Развивая идеи межвузовского образовательного проекта «Научный диалог с нобелевскими лауреатами по физике» исследуем возможность разработки компьютерной анимации динамических процессов с визуализацией фундаментальных математических моделей в области современной физики и физической электроники.
Нобелевская премия по физике 1997 года присуждена группе исследователей - Стивену Чу, Уильяму Филипсу (США) и Клоду Коэн-Таннуджи (Франция) за работу по лазерному охлаждению атомов. Им удалось достичь температуры на несколько миллионных долей градуса выше абсолютного нуля.

Рисунок 1. Нобелевские лауреаты по физике 1997 г.:
Стивен Чу, Уильям Филипс (США) и Клод Коэн-Таннуджи (Франция)
В микромире мерой температуры служит средняя кинетическая энергия частицы. Наибольший вклад в энергию дает скорость поступательного движения частицы, значительно меньший - частота ее собственных колебаний. Чем быстрее движется и чаще колеблется частица, тем она "горячее". Даже при температуре 3 кельвина (почти -270оС) скорость атома составляет около 100 метров в секунду. Чтобы "заморозить" атом, его нужно остановить, вернее, понизить его скорость до сантиметров в секунду. Сделать это можно разными способами, но самым удобным оказался метод лазерного охлаждения.
В 1985 году У. Филипс начал серию достаточно успешных экспериментов по лазерному охлаждению атомов натрия. Но по мере уменьшения скорости атомов падает доплеровский сдвиг частоты их колебаний и метод становится неэффективным. Известно было, однако, что в магнитном поле резонансная частота атома возрастает, и это явление сумел использовать Филипс. Пропуская пучок атомов сквозь неоднородное магнитное поле, он компенсировал уменьшение эффекта Доплера и "затормозил" пучок. Отдельные его атомы охладились до температуры 50 милликельвин (50.10-3 К).
Следующим шагом стали работы С. Чу, который поместил шесть лазеров на стенках кубической камеры и сфокусировал лазерное излучение в ее центре. Теперь излучение замедляло атом при любом направлении его движения. Это выглядело так, словно он проходил сквозь очень вязкую жидкость, вроде меда. Так удалось достичь температуры 240 микрокельвин (240.10-6 К) и скорости атомов натрия около 30 см/сек. По грубым оценкам, эта величина была теоретическим пределом возможностей доплеровского метода охлаждения. Однако уже в 1988 году группа Филипса каким-то образом сумела "нырнуть" под этот предел, охладив группу атомов натрия до 40 микрокельвин (40.10-6 К).
Суть происшедшего объяснил К. Коэн-Таннуджи. Он показал, что в установке Филипса лазерные лучи создали серию стоячих волн поляризованного света, электрические поля которых напоминали своего рода гребенку. Когда атом проходит сквозь нее, всплески электрического поля поочередно "сбрасывают" атом во все более и более низкое энергетическое состояние и все сильнее и сильнее охлаждают его. Атом как бы все время движется в «гору», против поля, и теряет энергию. Этот метод получил название "сизифово охлаждение". Рекордное значение температуры получила группа К. Коэн-Таннуджи в период 1988-1995 годов. Ученым удалось охладить атомы гелия до температуры 0,18 микрокельвина (0,18.10-6 К), понизив их скорость до 2 см/сек.

Рисунок 2. Профиль распределения скоростей атомов
при трехмерном охлаждении

Рисунок 3. Лазерное охлаждение атомов в периодической таблице химических элементов
Эти работы уже нашли применение во многих областях физики. На основе охлажденных атомов создаются сверхточные эталоны времени. В управляемых атомных пучках можно наблюдать интерференцию частиц, получаемую до сих пор только на электромагнитных волнах, и с ее помощью измерять, например, очень малые изменения силы тяжести (см. "Наука и жизнь" № 10, 1997 г.). И, что еще важнее, лазерное охлаждение позволит получить и исследовать так называемый бозе-эйнштейновский конденсат - принципиально новое состояние вещества (см. "Наука и жизнь" № 5, 1996 г.).
Другая деятельность в неожиданном "астрофизическом" направлении заключается в создании "черной дыры" в бозе-конденсате: объекте, способном втягивать внутрь себя падающие звуковые волны. Такой объект пока не реализован в эксперименте, однако из-за многообещающих перспектив исследования продолжаются.
В проекте предлагается классическая иллюстрация динамики в поле стоячей волны, приводящей к охлаждению атомов, как задача о движении частицы по профилированной поверхности или контуру.

Рисунок 4. Иллюстрация лазерного охлаждения атомов
С давних пор было известно, что вещества могут существовать в виде твердых (кристаллических) тел, жидкости, газа и плазмы - в целом нейтральной смеси положительно и отрицательно заряженных частиц. Нобелевской премии по физике 2001 года удостоены американские исследователи Эрик А. Корнелл (Eric A. Cornell), Вольфганг Кеттерле (WolfgangKetterle) и Карл Е. Вейман (Carl E. Wieman) за получение и исследование свойств пятого состояния вещества - так называемого бозе-эйнштейновского конденсата.
Подробнее см.: https://www.nkj.ru/archive/articles/3801/ (Наука и жизнь, НОБЕЛЕВСКИЕ ПРЕМИИ 2001 ГОДА. ПЯТОЕ СОСТОЯНИЕ ВЕЩЕСТВА)
Американские исследователи получили бозе-эйнштейновский конденсат из нескольких миллионов атомов рубидия (87Rb) и натрия (23Na), охладив их до температуры 100 нанокельвинов, на десятимиллионную часть градуса выше абсолютного нуля (см. "Наука и жизнь" №5, 1996 г.). Впоследствии температуру удалось довести до 20 нанокельвинов. Охлаждение проводилось лазерным методом, разработанным нобелевскими лауреатами 1997 года С. Чу, У. Филипсом и К. Коэн-Таннуджи (см. "Наука и жизнь" №1, 1998 г.).Любая частица одновременно проявляет и волновые свойства. Электромагнитное излучение имеет квантовую природу, а, например, электроны, типичные элементарные частицы, испытывают дифракцию - чисто волновое явление. Длина волны, связанной с частицей, зависит от ее квантового состояния. Бозе-эйнштейновский конденсат должен вести себя как единая волна. Разделив облако конденсированных атомов на две части, исследователи получили две волны, которые образовали картину интерференции. Это и свидетельствовало, что волны когерентны и, следовательно, действительно был получен бозе-эйнштейновский конденсат из атомов, находящихся в одном квантово-механическом состоянии.

Рисунок 5. Нобелевские лауреаты по физике 2001 г.
Эрик А. Корнелл (Eric A. Cornell), Вольфганг Кеттерле (WolfgangKetterle) и Карл Е. Вейман (Carl E. Wieman)
«Снимаем динамический хаос атомов»
Чтобы сделать чёткий фотоснимок, затвор современной цифровой камеры можно открыть на четырёхтысячную долю секунды. Но чтобы заглянуть внутрь вещества и запечатлеть активность атомов, нужен фотоаппарат с затвором, который срабатывает в миллионы раз быстрее.
Именно такое устройство придумали исследователи из Columbia Engineering и Университета Бургундии — оно снимает с выдержкой в триллионную долю секунды. Стоит понимать, что этот «затвор» — не механическое устройство, а лишь метафора. Для изучения вещества в новой «камере» используется взаимодействие не с фотонами света, как в обычном фотоаппарате, а с нейтронами. Сконструированная учёными установка позволяет запечатлеть важное физическое явление — динамический хаос.
Простыми словами, динамический хаос — это изменение положения атомов в кристалле, которые хаотически движутся или «танцуют» определённым образом в короткие промежутки времени — например, под действием вибрации или изменения температуры. Это явление, которое мы ещё не до конца понимаем, имеет решающее значение для изучения свойств и реакций веществ. Сегодня мы можем использовать для таких исследований методы кристаллографии, однако новая «фотокамера» помогает изучать материалы с невиданной ранее детальностью.
Понимание природы динамического беспорядка в материалах поможет нам создавать более энергоэффективные термоэлектрические устройства — твердотельные холодильники и тепловые насосы, лучше извлекать полезную энергию из отработанного тепла, такого как выхлопы автомобилей и выбросы электростанций, путём преобразования его в электричество. А ещё — разрабатывать более совершенные материалы и оборудование для электрического питания марсоходов в условиях нехватки солнечного света.

Картинка, сгенерированная нейросетью по описанию "«Камера» с выдержкой в одну триллионную долю секунды фиксирует динамический хаос атомов"
Ключевая особенность новой «камеры» — переменная выдержка. Неупорядоченные скопления атомов постоянно движутся, и когда команда использовала медленный затвор, динамический беспорядок выглядел размытым. Новый метод, позволяющий получать чёткие изображения, учёные назвали variable shutter PDF или vsPDF.
Вещество изучается с помощью рассеяния нейтронов на атомах кристаллической решётки. Измеряя параметры нейтронов, рассеянных на атомах вещества, можно построить функцию распределения атомов по уровням энергии (PDF, Pair Distribution Function). Дальше, чтобы получить полную картину, нужно проинтегрировать эту функцию по всем возможным энергиям за некоторый промежуток времени. Именно промежуток времени, за который интегрируется энергия этих функций, и является в данной работе аналогом «скорости затвора». Варьируя длину таких промежутков, учёные могут отличить динамические колебания атомов, которые проявляются только в короткие отрезки времени, от каких-то более долговременных изменений в кристаллической структуре вещества.
Исследователи уже испытали свою камеру на материале под названием теллурид германия (GeTe), который из-за его особых свойств применяется для преобразования отработанного тепла в электричество или для использования электричества в целях охлаждения.
Камера показала, что структура GeTe в среднем оставалась полностью упорядоченной при любых температурах. Но при сильном нагревании он демонстрировал динамический беспорядок, когда атомы смещались относительно своих нормальных положений в кристаллической решётке, следуя градиенту, который соответствует направлению спонтанной электрической поляризации материала.

Иллюстрация, показывающая атомную структуру GeTe при более длинной (слева) и более короткой (справа) выдержках (Джилл Хемман / ORNL, Министерство энергетики США)
Сейчас учёные работают над тем, чтобы упростить использование новой технологии в разных областях науки и применить её к другим системам с динамическим беспорядком. Вскоре этот метод можно будет использовать во многих материальных системах, где важна атомная динамика, — от наблюдения за движением лития в электродах батареи до изучения динамических процессов при расщеплении воды солнечным светом.
Кино в науке: научный видеоконтент в кадрах компьютерной анимации
Разработан компьютерно-графический метод анимационного моделирования экспериментальных измерений в задачах физической электроники (на примере «сизифово» охлаждения атомов в квантовой электронике и стохастических процессов в твердотельной электронике).
Для проведения этого исследования было использовано современное программное и математическое обеспечение, включая интерактивную графику системы компьютерной математики Maple. Были разработаны алгоритмы и комплекс программ для анимационного моделирования динамики частиц на профилированной поверхности и случайных блужданий на плоскости.
Разработанный комплекс программ целесообразно использовать в научной работе при изучении методов математического и компьютерного моделирования с медиаконтентом, методов визуализации и макетирования, экспериментальных измерений на основе интеграции технических и творческих направлений подготовки.
Анимационные модели диффузионных процессов в твердотельной электронике
Для того чтобы получить четкий фотоснимок, затвор современной цифровой камеры способен открыться за четыре тысячные доли секунды. Однако, чтобы проникнуть внутрь вещества и зафиксировать активность атомов, необходимо обладать фотоаппаратом с затвором, который срабатывает в миллионы раз быстрее.
Такое устройство было создано исследователями из Columbia Engineering и Университета Бургундии. Оно способно делать снимки с выдержкой в триллионную долю секунды. Важно отметить, что это "затвор" не является механическим устройством, а скорее метафорой. Для изучения вещества в этой новой "камере" используется взаимодействие не с фотонами света, как в обычном фотоаппарате, а с нейтронами. Спроектированная учеными установка позволяет зафиксировать важное физическое явление – динамический хаос [17].
Другими словами, динамический хаос представляет собой непредсказуемое движение атомов в кристалле, когда они перемещаются случайным образом или совершают определенные "танцы" в короткие отрезки времени, возникающие, например, под воздействием вибрации или изменения температуры. Это явление, которое еще не до конца объяснено, играет ключевую роль в изучении свойств и реакций веществ. В настоящее время для таких исследований мы можем использовать методы кристаллографии, но новое "фотооборудование" открывает возможность изучать материалы с невиданной ранее точностью.
Понимание динамического беспорядка в материалах поможет усовершенствовать термоэлектрические устройства, такие как твердотельные холодильники и тепловые насосы, для более эффективного извлечения полезной энергии из отходящего тепла, такого как выхлопы автомобилей и выбросы электростанций, путем его преобразования в электричество. Кроме того, это позволит разрабатывать более совершенные материалы и оборудование для обеспечения электропитания марсоходов в условиях ограниченной солнечной активности.
Одной из ключевых особенностей новой «камеры» является возможность изменения выдержки. Атомы, находящиеся в беспорядке, постоянно двигаются, и когда исследователи использовали медленный затвор, динамический хаос выглядел размытым. Этот новый метод, обеспечивающий получение четких изображений, был назван учёными variable shutter (переменным затвором) PDF или vsPDF.
С помощью рассеяния нейтронов на атомах кристаллической решетки исследуются свойства вещества. Путем измерения параметров рассеянных нейтронов на атомах можно получить функцию распределения атомов по уровням энергии, известную как PDF (Pair Distribution Function). Чтобы получить полное представление, необходимо проинтегрировать эту функцию по всем возможным энергиям в определенный временной интервал. Этот временной интервал, по которому производится интегрирование энергии функций, аналогичен "скорости затвора" в данном исследовании. Путем изменения длины этих интервалов ученые могут выделить динамические колебания атомов, проявляющиеся лишь в короткие отрезки времени, от более долговременных изменений в кристаллической структуре вещества.
Исследователи уже провели испытания своей камеры на материале, известном как теллурид германия (GeTe), который благодаря своим уникальным свойствам используется для преобразования отходящего тепла в электричество или для использования электрической энергии в целях охлаждения.
Изображение показало, что структура GeTe оставалась упорядоченной при всех температурах, за исключением случаев с высоким нагреванием, когда проявлялся динамический беспорядок. При этом атомы смещались относительно своих обычных позиций в кристаллической решетке, двигаясь вдоль градиента, соответствующего направлению спонтанной электрической поляризации материала.
Многие явления в области физики и естественных наук могут быть описаны с использованием случайных блужданий и соответствующих предельных процессов, известных как диффузионные процессы. Диффузия представляет собой перемещение атомов в среде в определенном направлении и происходит как в твердых телах, жидкостях, так и газах даже без внешнего воздействия. Философское объяснение данного экспериментально наблюдаемого явления заключается в том, что предел случайных блужданий отражает микроскопическую природу ситуации. Даже в случае полностью детерминированных микроскопических систем могут возникать хаотические, казалось бы, случайные движения, которые практически неотличимы от тех, что происходят в результате случайного процесса.
Диффузионные процессы являются ключевыми во многих явлениях, связанных с твердыми телами, а также в процессах кинетики микроструктурных изменений во время металлургической обработки и использования. Типичные примеры включают фазовые превращения: рекристаллизация; окисление; ползучесть; спекание; ионная проводимость; перемешивание в тонкопленочных устройствах; прямое технологическое использование диффузии, включающее твердые электролиты для современных приложений аккумуляторов и топливных элементов; изготовление полупроводниковых чипов и микросхем.
Точечные дефекты в кристаллической решетке
Одно из первых объяснений природы случайного блуждания принадлежит Карлу Пирсону. описавшего его в 1905 году. Более физическое объяснение подхода к пониманию случайного блуждания содержится в статье Альберта Эйнштейна того же года.
На рисунке N случайное блуждание начинается с точки , потом выбирается случайное направление в двухмерном пространстве, затем совершаются шаги на расстояние 1 по прямой в любое направление, а далее процесс повторяется бесконечное количество раз. Такой случайный процесс можно представить в виде траектории кусочно-линейной кривой.
Случайные блуждания Пирсона на плоскости
При анализе некоторых классических явлений, предполагалось, что каждый атом связан с конкретным узлом кристаллической решетки. Также считалось, что атом ограничивается лишь тепловыми колебаниями вокруг своего среднего положения. Однако на самом деле атомы обладают большей подвижностью и способны переходить с одного узла решетки на другой. Основной механизм диффузии заключается в перемещении отдельных частиц или их небольших групп на расстояния, сравнимые с межатомными интервалами.
Процессы диффузии играют особую роль в тонкопленочных структурах, состоящих из различных слоев материалов. Эти структуры являются основой практически всех микроэлектронных устройств. В отличие от изменений в составе массивных материалов, которые имеют место при взаимной диффузии в толстых слоях, мало влияющих на их свойства, в тонкопленочных композициях подобные процессы могут радикально изменить состав и структуру отдельных слоев. Это, в свою очередь, может привести к ухудшению характеристик устройств и интегральных схем, а также к их выходу из строя.
Анимационные динамические модели на профилированной поверхности (иллюстрация «сизифово» охлаждение атомов светом)
Далее будут описаны физические и математические принципы, на основе которых будут созданы анимационные динамические модели для решения задач о движении частицы по профилированной поверхности или контуру. Описанные принципы базируются на классической модельной системе движения атомов.
Попробуем рассмотреть «cизифово» охлаждение одиночного связанного атома, внутренняя структура которого представлена тремя уровнями: уровень g – основное состояние атома; уровень e – возбужденное состояние атома; уровень r – состояния накопленной энергии. Переход состояния атома из уровня g в уровень e является электрическим дипольным переходом, произошедший благодаря возбуждаемым лазерным лучом стоячей волны, частота которого была настроена чуть выше резонансной частоты для перехода в состояние δ, где частоты выражены в радианах на секунду. Далее уровень e самопроизвольно распадается со определенной скоростью до уровня r с долей разветвления β и до уровня g с долей разветвления 1-β.
Предположим, что интенсивность лазера и его перестройка имеют такие значения, что доля времени, которую атом проводит в возбужденном состоянии, ничтожна мала, а скорость перехода состояния атома с уровня r в уровень g составляет R(r→g)=1/Tr , где Tr – короткое время продолжительности переноса. Из этого можно предположить, что положение иона не изменяется во время передачи энергии [34].
Сам атом ограничен одним измерением (в направлении x) гармонической ямой U0(x), которая характеризуется частотой колебаний самого атома. Значение U0 считается внешним потенциалом, который не зависит от лазерного луча. В тот момент, когда атом самопроизвольно распадается с уровня e, направление испускания фотонов считается параллельным (или перпендикулярным) движению атома.
Исходя из того, что энергии перехода описываются следующим неравенством Ee-Eg≫|Er-Eg|, то Сизифово охлаждение описывается простыми математическими выражениями. Такие упрощения качественно не повлияют на результаты для других, более сложных случаев. Сизифово охлаждения объясняется ключевым моментом: энергии одетых состояний или подуровней основного состояния со смещенным светом изменяются в зависимости от направления движения атомов. Такая ситуация будет достигнута в нашей модели, если взять интенсивность лазера, которая линейно изменяется в зависимости от x в диапазоне движение атомов, а градиент интенсивности обусловлен лазерной стоячей волной в направлении x.
Модельная система атома с тремя внутренними энергетическими уровнями g, e и r: лазерный луч стоячей волны поднимает частоту уровня g на частоту уровня e выше своей резонансной частоты, уровень e снижается с разветвлением фракции β до уровня r и с разветвлением фракции 1-β до уровня g .
Далее, произведем классическое моделирование электрического поля лазера [34]:
Esum=(Emax/2)[cos(kx-wt)+cos(kx+wt) ]=Emaxcos(wt)cos(kx)
где x – положение атома и волнового числа k=2π/λ ( λ– длина волны лазера).
Согласно данному уравнению, интенсивность лазерного излучения I(x) изменяется по закону cos2(kx), как показано на рисунке. Сизифово охлаждение будет наиболее эффективным, когда градиент интенсивности будет максимальным; это происходит в точке половинной интенсивности стоячей волны. Поэтому мы предполагаем, что среднее положение атома находится вблизи x=π/4k [34].
Ограничение атома одномерной гармонической ямой
Линейное изменение светового сдвига уровня g относительно x в диапазоне движения атома следует из предположения о локализации: протяженность движения атома меньше λ/2π (режим Лэмба-Дикке).
На основании описанных алгоритмов проведем программирование в среде Maple для создания анимации динамической модели на профилированной поверхности. Интерфейс анимации представлен на рисунке.
Интерфейс анимационной динамической модели на профилированной поверхности
Библиографический список
- Бутиков Е.И., Кондратьев А.С. Физика: В 3 кн. Кн.1. Механика. – М.: Физматлит, 1994. - 368 с.
- «Прыжок рыси». Материалы сайта YouTube URL: https://youtu.be/DqQIoA1ijzQ (дата обращения: 10.01.2024).
- Европейская рысь. Материалы сайта «Кошачьи». URL: https://felidae-g2n.jimdofree.com/lynx/lynx-lynx/l-l-lynx/ (дата обращения: 10.01.2024).
- Нестерова Е.И. Средства и технологии макетирования в медиаиндустрии: учебное пособие. – СПб.: СПбГИКиТ, 2017. - 131 с.
- Скворцов А.И., Фишман А.И. Видеозадачник: от наблюдения к измерению. URL: http://booksee.org/book/814974 (дата обращения: 9.01.2024).
- Ходанович А.И., Соколов Д.А., Сорокина И.В., Штейн Б.М. Демонстрационный эксперимент и прецизионные измерения с маятником Фуко. Физика в школе и вузе. Международный сборник научных статей. Вып.21.- СПб.: РГПУ им. А.И. Герцена, 2019. – С 54 - 59.
- Ходанович А.И., Штейн Б.М., Кондыбаева И.Ш. Совершенствование методической системы обучения физике в профессиональной подготовке киноинженеров / Современные проблемы науки и образования.- М.: РАЕ, 2022.- № 3, 0.5 п.л. URL: https://science-education.ru/ru/article/view?id=31835 (дата обращения: 20.01.2024).
- Ходанович А.И., Сорокина И.В., Штейн Б.М., Перелыгин С.В., Соколов Д.А. Аудиовизуальные технологии в медиаискусстве: монография // под общ. ред. А. И. Ходановича- Санкт-Петербург: СПбГИКиТ, 2022. – 279 с. – ISBN 978-5-94760-494-8.
- Ходанович А.И., Сорокина И.В. Проблема формализма знаний в профессиональной подготовке инженеров в кинообразовании. Актуальные вопросы развития индустрии кино и телевидения в Современной России. Материалы II Национальной научно-практической конференции (СПб., 25 октября 2019 г.).- СПб.: СПбГИКиТ, 2019.-
С 74-76. - Ходанович А.И., Сорокина И.В. Физическая симметрия и масштабные преобразования в цифровом кинематографе. Актуальные вопросы развития индустрии кино и телевидения в современной России. Материалы I Национальной научно-практической конференции 26, 27 июня 2018 г.- СПб.: СПбГИКиТ, 2018.- С 39-42.
- Ходанович А.И. Приоритеты компетентностного подхода в современном медиаобразовании. Инновационные технологии в медиаобразовании: материалы II Международной научно-практической конференции, 29, 30 мая 2017 г. / редкол. : А. И. Ходанович (отв. ред.) [и др.]. - СПб. : СПбГИКиТ, 2018. – С 19-22.
- Ходанович А.И., Сорокина И.В., Соколов Д.А. Формирование инженерного мышления в кинообразовании. Актуальные вопросы развития индустрии кино и телевидения в современной России: сб. науч. трудов, посвященный Году российского кино. Ч.1.- СПб.: СПбГИКиТ, 2016.- С 80-87.
Проект: «Кино в науке: научный видеоконтент в кадрах компьютерной анимации»
2025 г.
Асимптотические функции в анимации статистических распределений при обработке эмпирических данных
Обычно для измерения некоторой физической величины в эксперименте производят несколько измерений, а затем находят среднее арифметическое полученных чисел, которое принимают за приближенное значение измеряемой величины. Предполагая, что измерения производятся в одних и тех же условиях, можно показать, что среднее арифметическое дает результат более надежный, чем отдельные измерения, и с увеличением числа измерений надежность этого результата возрастает. Отдельные измерения дают неодинаковые значения измеряемой физической величины. Результат каждого измерения зависит от многих случайных причин, которые не могут быть заранее полностью учтены.
Среднее арифметическое случайных величин имеет меньшее рассеяние, чем каждая отдельная величина. Иначе говоря, среднее арифметическое оказывается более близким к истинному значению измеряемой величины. Действительно, из свойств дисперсии следует, что среднее квадратичное отклонение среднего взаимно независимых измерений случайной величины в раз меньше среднего квадратичного отклонения каждого измерения в терминах случайных величин, т.е. σ()=σ/√n . Кроме того в силу теоремы Чебышева для случайных величин с ограниченной дисперсией различия между средним и неизвестным истинным значением измеряемой величины (математическим ожиданием) сколь угодно малы при неограниченной выборке измерений, т.е. Limn→∞P(|-M(X)|<ε)=1.
Оказывается, что по данным выборки можно построить случайную величину (ее возможные значения будем обозначать через t): Е=(-a)/(S/√n), которая имеет распределение Стьюдента с k = n-1 степенями свободы; здесь - выборочная средняя, S- среднее квадратичное отклонение, п- объем выборки. Плотность распределения Стьюдента, S(t, n)=Bn(1+t2/(n-1))-n/2, где Bn=(Г(n/2))/√(π(n-1))*Г((n-1)/2). Заметим, что Г(n+1)=n!, поэтому вводить Г- функцию можно не прибегая к определению спецфункции.
Из предельных соотношений Limn→∞Bn=1/(√2π); Limn→∞(1+t2/(n-1))-n/2=e-t^2/2, следует, что при неограниченном возрастании объема выборки распределение Стьюдента стремится к нормальному закону (рис.1).
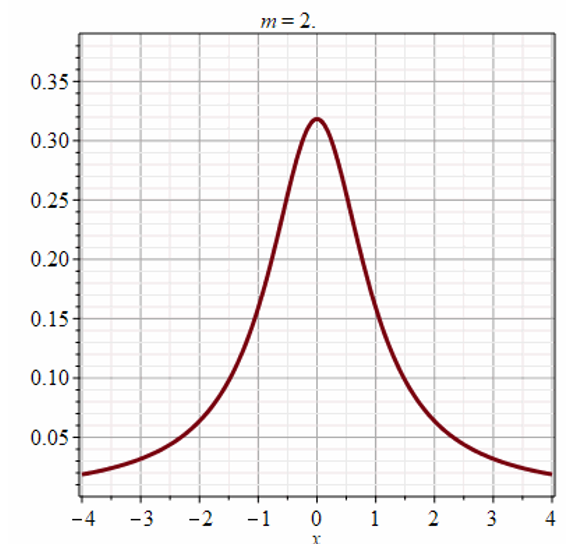
Рис.1 Фрагмент анимации распределения Стьюдента в среде Maple
Мы видим, что распределение Стьюдента определяется параметром n - объемом выборки (или числом степеней свободы k = n - 1) и не зависит от неизвестных параметров а и σ; эта особенность является его достоинством. Поскольку S(t,n) - четная функция от t, вероятность осуществления неравенства |(-a)/(S/√n)|<ϒ определяется следующим образом:
![]()
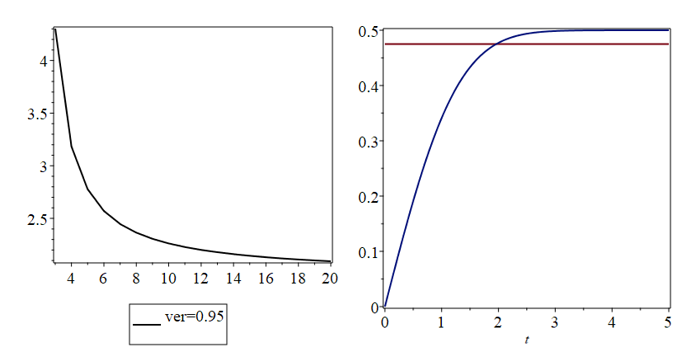
Рис.2. Графический метод определения асимптотического коэффициента Стьюдента
Итак, пользуясь распределением Стьюдента, мы нашли доверительный интервал (-tγs/√n<a<+tγs/√n)=γ, покрывающий неизвестный параметр а с надежностью γ. Здесь s=√(((xi-)2)/(n-1))- среднее квадратичное отклонение. На компьютере (например, в среде Maple) по заданным n и γ рассчитываем tγ. Причем, при большой выборки данных, характерной для компьютерного эксперимента плотность распределения Стьюдента можно заменить асимптотической функцией Гаусса, т.е. S(t,n)=1/(√(2π))*e(-t^2)/2, а стандартное отклонениеs=√D(x) . Таким образом, асимптотический коэффициент Стьюдента является графическим или численным решением уравнения 1/2*erf(t/√2)=γ/2, где erf - функция ошибок, γ - доверительная вероятность (рис. 2).
Анимация гауссовой функции с асимптотикой нормального распределения
Нормальный закон распределения (часто называемый законом Гаусса, или функцией Гаусса) играет исключительно важную роль в науке и занимает среди других законов распределения особое положение. Это- наиболее часто встречающийся в теории и практике закон распределения, например, в оптике или атомной спектроскопии (рис.1, 2). Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях. Отметим, что расширенные средства графики распространенных математических пакетов обеспечивают наглядность при изучении вероятностно- статистических моделей и методов с помощью компьютера.
Рис. 1. Иллюстрация гауссова пучка в оптике
Согласно центральной предельной теореме сумма достаточно большого числа независимых (или слабо зависимых) случайных величин, подчиненных каким угодно законам распределения (при соблюдении некоторых весьма нежестких ограничений), приближенно подчиняется нормальному закону, и это выполняется тем точнее, чем большее количество случайных величин суммируется.
Большинство встречающихся на практике случайных величин, таких, например, как ошибки физических измерений, могут быть представлены как суммы весьма большого числа сравнительно малых слагаемых- элементарных ошибок, каждая из которых вызвана действием отдельной причины, не зависящей от остальных. Каким бы законам распределения ни были подчинены отдельные элементарные ошибки, особенности этих распределений в сумме большого числа слагаемых нивелируются, и сумма оказывается подчиненной закону, близкому к нормальному.
Математические законы теории вероятностей не являются беспредметными абстракциями, лишенными физического содержания; они представляют собой математическое выражение реальных закономерностей, фактически существующих в массовых случайных явлениях природы.
Оперируя такими понятиями, как события и их вероятности, случайные величины, их законы распределения и числовые характеристики, теория вероятностей дает возможность теоретическим путем определять вероятности одних событий через вероятности других, законы распределения и числовые характеристики одних случайных величин через законы распределения и числовые характеристики других. Такие косвенные методы позволяют значительно экономить время и средства, затрачиваемые на эксперимент, но отнюдь не исключают самого эксперимента. Каждое исследование в области случайных явлений, как бы отвлеченно оно ни было, корнями своими всегда уходит в эксперимент, в опытные данные, в систему наблюдений.
Разработка методов регистрации, описания и анализа статистических экспериментальных данных, получаемых в результате наблюдения массовых случайных явлений, составляет предмет специальной науки- математической статистики. Все задачи математической статистики касаются вопросов обработки наблюдений над массовыми случайными явлениями, но в зависимости от характера решаемого практического вопроса и от объема имеющегося экспериментального материала эти задачи могут принимать ту или иную форму.
Закономерности, наблюдаемые в массовых случайных явлениях, проявляются тем точнее и отчетливее, чем больше объем статистического материала. При обработке обширных по своему объему статистических данных часто возникает вопрос об определении законов распределения тех или иных случайных величин. Теоретически при достаточном количестве опытов свойственные этим случайным величинам закономерности будут осуществляться сколь угодно точно. На практике нам всегда приходится иметь дело с ограниченным количеством экспериментальных данных; в связи с этим результаты наших наблюдений и их обработки всегда содержат больший или меньший элемент случайности.
Возникает вопрос о том, какие черты наблюдаемого явления относятся к постоянным, устойчивым и действительно присущи ему, а какие являются случайными и проявляются в данной серии наблюдений только за счет ограниченного объема экспериментальных данных. Естественно, к методике обработки экспериментальных данных следует предъявить такие требования, чтобы она, по возможности сохраняла типичные, характерные черты наблюдаемого явления и отбрасывала все несущественное, второстепенное, связанное с недостаточным объемом опытного материала. В связи с этим возникаем характерная для математической статистики задача сглаживания или выравнивания статистических данных, представления их в наиболее компактном виде с помощью простых аналитических зависимостей.
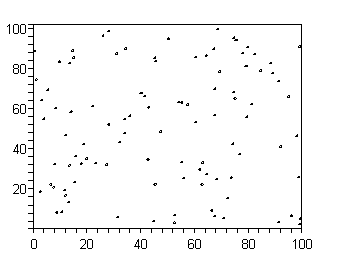
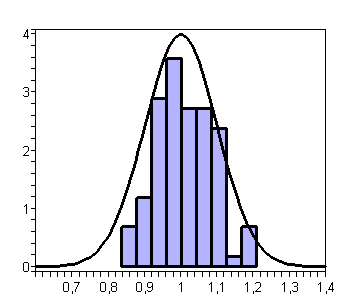
Рис. 2. Модель доплеровского уширения
спектральных линий атомов


Рис.3 Кадры анимации гауссовой функции с асимптотикой
нормального распределения

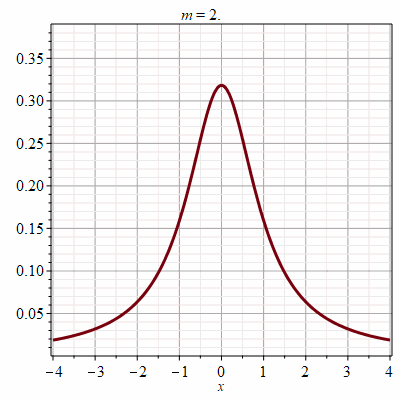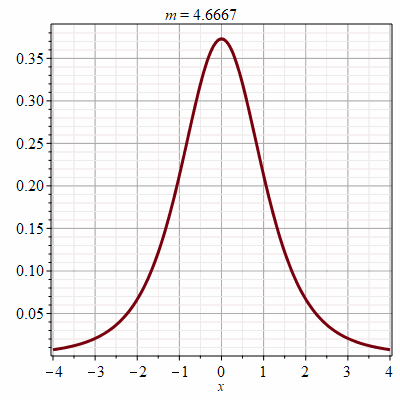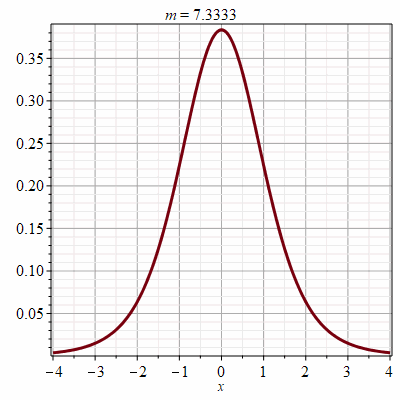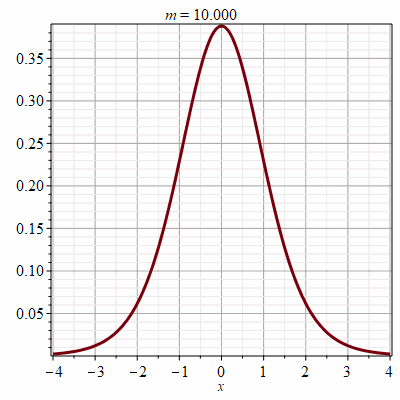
Рис. 4. Анимации
Имитационное моделирование мониторинга воздушных линий связи в задачах интеллектуальной электротехники

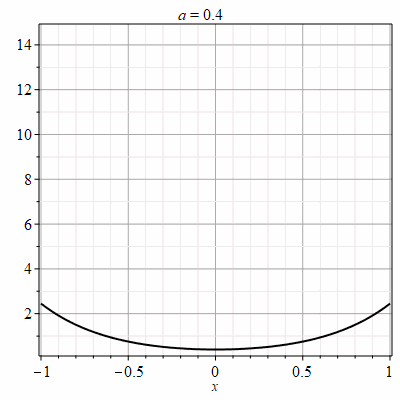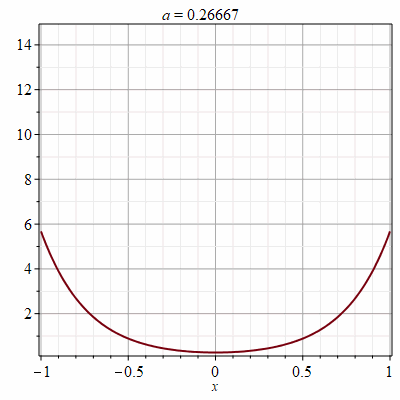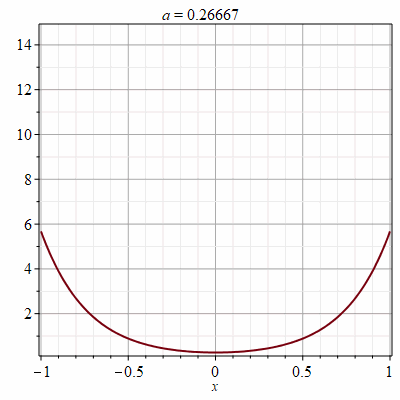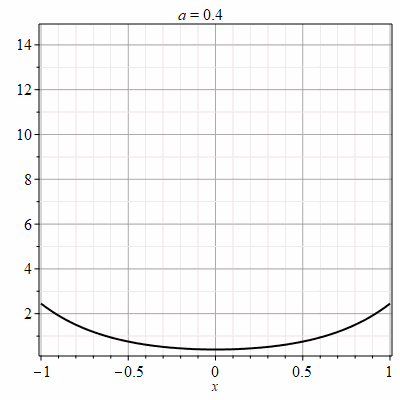
Рис.1 Фрагмент анимации цепной линии в имитационной модели мониторинга воздушных линий связи
Одной из основных задач Стратегии развития Единой национальной электрической сети является повышение эффективности функционирования воздушных линий электропередачи и линий связи. Решение данной задачи предполагает внедрение со временных систем мониторинга технического состояния воздушных линий электропередачи и линий связи. Требуются и более строгие методики расчета состояния оборудования, позволяющие учесть внешние климатические факторы. Приведен анализ существующих методов определения текущего состояния провода воздушной линии электропередачи. Установлено, что однозначное общепринятое решение рассматриваемой проблемы отсутствует.
Проведено теоретическое исследование, показавшее необходимость объединения предлагаемых решений. С учетом полученных другими исследователями результатов разработана анимационная модель в интерактивной среде Maple, позволяющая проводить оценку текущего состояния провода на основе данных с сенсоров. С помощью модели можно определить стрелу провеса, длину провода, натяжение провода, удельный вес провода в условиях бокового ветра и гололедно-изморозевых отложений. Одновременно модель с цепной линией позволяет определять оптимальные значения натяжения для каждого пролета индивидуально в зависимости от воздействия внешних факторов. На основе имитационной модели показана возможность организации системы текущего мониторинга проводов в пролете. Сравнительный анализ текущего состояния проводов и грозозащитных тросов и их предельных значений позволит провести оценку эффективности мероприятий по предотвращению аварийных ситуаций.
Проведена экспериментальная проверка имитационной модели мониторинга с цепной линией (ЦЛ) в задачах интеллектуальной электротехники:
- горизонтальное натяжение как инвариант ЦЛ;
- оптимальная длина ЦЛ в заданном пролете;
- статический метод определения ускорения свободного падения (удельного веса, длины и массы провода) с оценкой погрешностей.
Анимация цепной линии в формализме динамического метода
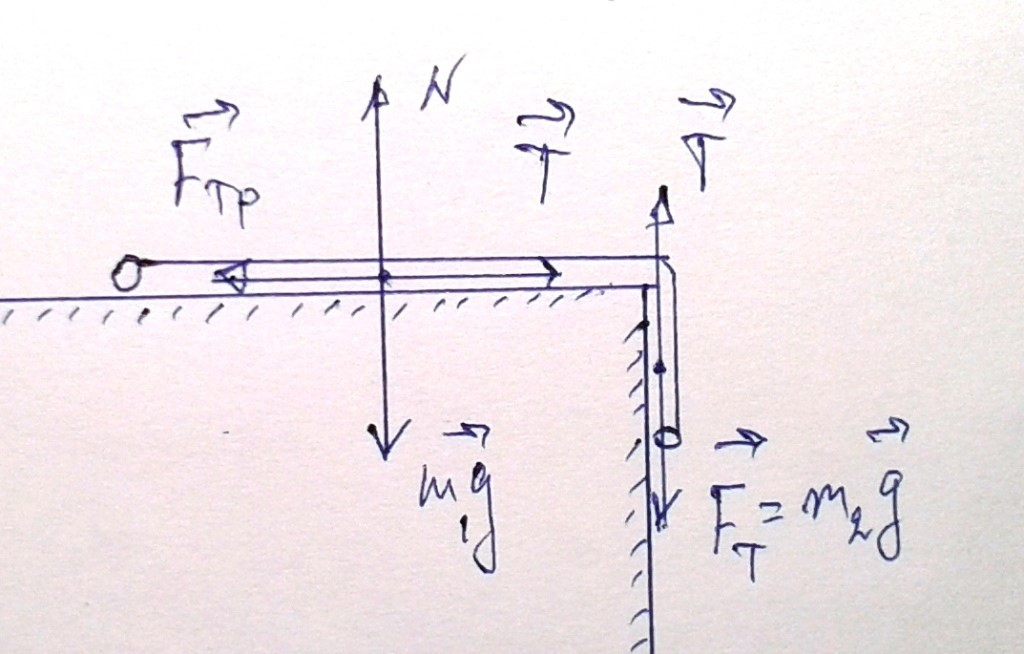
В настоящий момент, благодаря бурному процессу информатизации обучения, появилось большое количество пакетов прикладных программ, позволяющих автоматизировать решение различных задач, в том числе и физических. Постоянное использование подобных пакетов в процессе обучения теоретической физике может привести к формированию неверных представлений о методах, используемых в науке. В связи с этим возникает проблема сохранения первостепенной роли аналитических методов в сочетании с методами компьютерного моделирования при решении физических и технических задач.
Одним из таких методов решения динамических задач является метод разложения по кратным скобкам (мультискобкам) Пуассона, формулируемый в рамках гамильтонового подхода. Он позволяет получать точное решение в виде разложения в ряд Тейлора по степеням времени движения. Отметим, что гамильтонов подход, используемый в данной работе, является весьма употребительным в теоретической физике и на практике используется гораздо шире лагранжевого подхода (например, при рассмотрении статистической механики).
Применение алгебраического метода при решении задач классической динамики можно рассматривать как хорошее дополнение к курсу математического анализа, позволяющее глубже осваивать и совершенствовать технику дифференцирования функций. Предлагаемый подход легко переносится и на другие разделы теоретической физики.
Между тем, возможен подход к решению динамических задач, в котором аналитическое решение для консервативной системы может быть получено на основе использования только дифференциальных выражений, содержащих скобки Пуассона в виде разложения ряда Тейлора по степеням времени движения. При этом оказывается возможным нахождение решения для некоторых уравнений, недоступное в рамках непосредственного аналитического интегрирования, не говоря уже об удобстве таких решений по сравнению с решениями, полученными численными методами.
Рассмотрим задачу. Однородная цепочка длиной l свисает на величину x0 c края горизонтального стола, по которому она может скользить без трения. Найти зависимость x(t), если v0=0.
Эта задача имеет точное решение. Уравнение движения цепочки записывается в виде:
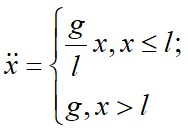
Решение уравнения при x>l соответствует равноускоренному движению:
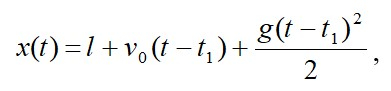 ,
,
где t - момент времени, в который вся цепочка принимает вертикальное положение, а v1 - ее скорость в этот момент времени.
Далее удобно ввести α=√g/l. Общее решение уравнения движения при x≤l записывается в виде:
![]()
При заданном начальном условии C1=C2=x0/2 решение принимает вид: x(t)=x0ch(α*t); t≤t1, где момент времени t1 определяется соотношением x(t)=x0ch(α*t1)=l, а значение v1 определяется следующим образом:
![]()
Интересно сопоставить это решение с решением, получаемым методом кратных скобок Пуассона в теоретической физике [7].
Записав функцию Гамильтона в виде:
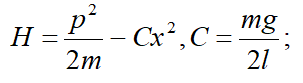
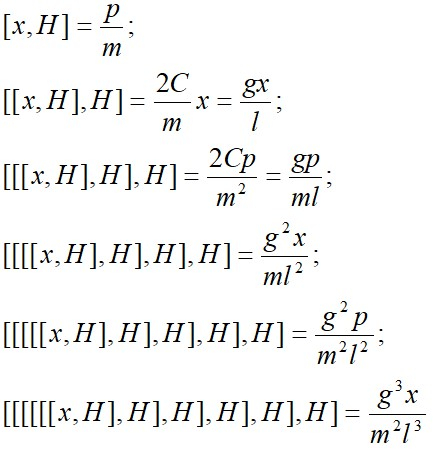
и т. д.
В результате получим разложение:
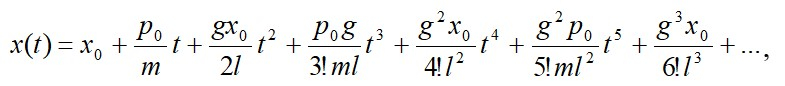
которое соответствует общему выражению при произвольных начальных условиях:
![]() .
.
Тогда
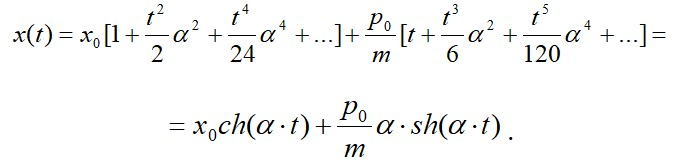
В частности, при заданных в условии задачи начальных условиях данное разложение сводится к известному выражению для гиперболического косинуса (цепной линии)
x(t)=x0ch(√(g/l)*t).
Заметим, что процедура вычисления и суммирования кратных скобок Пуассона может быть автоматизирована в среде символьной математики в рамках компьютерно-аналитического метода решения задачи.
Впервые в проекте решена динамическая задача о цепной линии с учетом трения, получена анимация координаты с коэффициентом трения в интерактивной среде символьной математики Maple.

Творческий проект в медиасфере:
«Системы управления художественным освещением театрального зала» (начало, 2024 г.)
Аннотация:
Световое сопровождение сценических постановок является одним из важнейших аспектов зрелищных мероприятий. Для проведения светового шоу важно обеспечить качественное управление осветительным оборудованием. Преподаватели КВТК и ГИКиТ СПб совместно с инженером отдела световой аппаратуры СПбГБУК «Театр Эстрады им. А.И. Райкина» Кариной Альбертовной Колумбаевой (выпускницей КВТК и ГИКиТ СПб) исследуют возможности современных систем управления осветительным оборудованием и способы повышения надёжности при передаче сигналов управления. Новый способ построения системы управления осветительной аппаратурой подразумевает использование беспроводной передачи команд. Такая система должна будет иметь большую устойчивость к радиопомехам и меньшую задержку передачи команд в сравнении с использовавшимися на зрелищных мероприятиях.
Библиографический этап творческого проекта
История сценического освещения
История развития сценического освещения берёт свое начало с Древней Греции. В те времена спектакли игрались под открытым небом, и существовало только естественное освещение в сочетании со световыми эффектами, создаваемыми с помощью огня и дыма. В эпоху Возрождения, когда театр был перенесён в закрытые помещения, в качестве источников света использовались сальные и восковые свечи. На смену свечам пришли масляные светильники. В металлический резервуар опускали круглый фитиль, прикрепленный к плавающему в масле поплавку.
|
Масляная лампа из Олимпийского театра в г. Виченза. Конец XVI в. Для получения цветного света использовалось окрашенное масло |
Масляная лампа с тремя фитилями из Олимпийского театра г. Виченза. Конец XVI в. Лампы расставлялось в кулисах на низких подставках |
В самом начале XVI века в Италии появился театр с перспективными декорациями. На сцене источники света укреплялись так, чтобы свет проникал через промежутки между отдельными декорациями и через окна передних фасадов. За источниками света устанавливали медный отражатель. В театре той поры использовались и сюжетные световые эффекты, такие как, например, молния, которая получалась при помощи вспышки, скользящей по натянутой проволоке. Архитектор Никола Саббатини (1574-1654) [1] в своей книге по театральному искусству описал различные механические способы затемнения, например, медленное опускание на огонь металлических труб или поворот вокруг огня металлического полуцилиндра.
|
Лампа с отражателями |
Механизм затемнения светильников |
В театре XVII в. встречалось также софитное освещение. Для подсветки использовались скрытые от зрителя источники света, установленные в проходах на каждом плане. В конце XVIII века масляные светильники были значительно усовершенствованы, появилось газовое освещение, яркость которого была уже на порядок выше. Газовое освещение широко распространилось в XIX в. С конца XIX в. электричество вытесняет газовое освещение. Однако новые источники света входили в театральную практику постепенно и на протяжении всего XIX в. сосуществовали с известными ранее.
На сегодняшний день без светового оформления не обходится ни одно сценическое пространство, а техническая база продолжает развиваться для облегчения управления приборами и выполнения любых нужд в области визуальных эффектов [2].
Особенности световой композиции
Одним из атрибутов современного искусства является сцена, на которой ставятся спектакли или выступают артисты. И здесь само освещение становится частью искусства, оно влияет на силу восприятия зрителями увиденного. Художник по свету должен чувствовать ритм и музыку. На зрелищных мероприятиях большое внимание уделяется именно динамике: перемещение лучей создаёт иллюзию движения на сцене даже при неподвижных выступающих.

Несколько типовых форм сцены: 1 – сцена-коробка; 2 – сцена-арена; 3 – пространственная сцена (а – открытая площадка, б – открытая площадка со сценой-коробкой); 4 – кольцевая сцена (а – открытая, б – закрытая); 5 – симультанная сцена (а – единая площадка, б – отдельные площадки)
Также большое значение в сценическом, и в частности концертном, освещении имеет цвет и его свойства. Важным свойством цвета является его теплота. Группу красных, оранжевых, жёлтых и жёлто-зелёных цветов принято называть тёплыми (по сходству с цветом солнца, огня), а голубо-зелёные, голубые, синие и фиолетовые цвета – холодными (по сходству со льдом, прохладной водой, небом и т.д.).
Существенный вклад в цветоведение внесли художники, философы и поэты. Величайший поэт И.В. Гёте (1749-1832) создал трактат «Учение о цвете». Все явления, связанные с цветом, Гёте рассматривал с позиции воздействия цвета на человека, выделяя два вида таких воздействий: физиологическое и психологическое. Гёте первым предложил чёткую систему, описывающую воздействие различных цветовых сочетаний на психику человека. Эмоциональные реакции на эти взаимоотношения являются эстетической основой цветовой гармонии. Шесть основных цветов образуют два треугольника. Первая характерная пара – жёлтый и синий – являлась основанием цветового треугольника, на вершине которого Гёте расположил «царственный» пурпурный цвет. Вторая характерная пара – оранжевый и фиолетовый – служила основанием треугольника, вершина которого отводилась «плебейскому» зелёному цвету. Таким построением Гёте впервые установил иерархию гармонических взаимосвязей.
Свернув линию спектра в кольцо, Гёте создал цветовой круг, где друг напротив друга оказались противоположные цвета. В «Шестицветном круге Гёте» три типа парных взаимосвязей: гармоническая, характерная и нехарактерная.
|
Гармонические пары цветов |
Характерные пары цветов |
Нехарактерные пары цветов |
|
пурпурно-зелёная фиолетово-жёлтая оранжево-синяя |
жёлто-синяя жёлто-пурпурная сине-пурпурная оранжево-фиолетовая оранжево-зелёная фиолетово-зелёная |
жёлто-зелёная жёлто-оранжевая оранжево-красная красно-фиолетовая фиолетово-синяя сине-зелёная |
По Гёте, эмоционально-выразительное значение цветов заключается в том, что противоположные цвета формируют ощущение умиротворяющей полноты. Гёте классифицировал типы колоритов, из которых выделил три основных: могучий, нежный и блестящий. В «могучем» преобладают активные «мажорные» красные тона, в «нежном» – пассивные «минорные» зелёно-синие, а в «блестящем» согласуются «мажорные» и «минорные» сочетания цветов круга.

Цветовые треугольники Гёте Цветовой круг Гёте
В дополнение к цветовому ряду Гёте немецкий живописец Филипп Отто Рунге (1777-1810) ввёл в систему цветовой гармонии светотональные отношения. Основой цветовой модели был оставлен цветовой круг Гёте, но пурпурный цвет заменён красным, а в саму систему введена чёрно-белая координата, превратившая двухмерную модель в трёхмерную. Эта модель отражает все три основных показателя цвета: цветовой тон, яркость и насыщенность. Помимо Рунге идею шестицветного цветоряда также развивали А. Шопенгауэр, В. Адаме, Э. Делакруа, А. Хёльцель, В. Ван Гог, В.В. Кандинский, П. Клее, И. Иттен и др.
Виды приборов художественного освещения
При постановке светотехнической композиции следует наиболее эффективно выбирать приборы с учётом их функций и возможностей управления. В зависимости от места установки осветительная аппаратура подразделяется на следующие основные виды: верхнего, горизонтального, бокового, выносного освещения, а также переносная аппаратура и аппаратура специального назначения (люстры, канделябры, фонари, проекционные приборы). Само сценическое освещение, как художественный приём, можно разделить на 3 вида:
|
Вид освещения |
Используемая аппаратура |
|
заливающий свет |
прожекторы с широким лучом, колорченджеры, прочие светильники |
|
точечный свет |
пушки, безлинзовые PAR, профильные прожекторы |
|
световые эффекты |
сканеры, лазеры, гобо-проекторы |
Наряду с приборами художественного освещения широко применяются приборы наполнения атмосферы, они предназначены для получения необходимой плотности и фактуры воздушного сценического пространства (генераторы дыма, тумана, снега, радуги, дождя, мыльных пузырей и др.).
При выборе подходящего оборудования для сценического освещения следует учитывать такие факторы, как:
1. количество выступающих;
2. стиль композиции;
3. ритм композиции;
4. тему и настроение композиции и пр.
От количества выступающих зависит количество необходимых световых приборов. Для одного исполнителя на сцене количество используемых приборов будет сведено к минимуму. В общем же случае световую программу необходимо выстроить таким образом, чтобы никто из артистов не остался в тени. От стиля музыки напрямую зависит вся световая композиция в целом. Например, классические концерты подразумевают статичное освещение исполнителей и создание максимального контраста с незадействованной частью сцены и залом. И, напротив, для рок-концертов характерен динамически изменяющийся свет. Цвет и движение лучей должны гармонично сочетаться с настроением музыки и транслировать ее слушателям. От ритма зависит скорость движения лучей и добавление эффекта стробирования.
В качестве примера ниже приведены фотографии приборов сценического освещения, используемые в художественно-постановочной части Театра Эстрады имени Аркадия Райкина. Парк оборудования регулярно пополняется, а руководство театра отправляет технический персонал на различные выставки современных решений технического оснащения сцены.
|
Генератор дыма Robe Faze 1050 FT [3]
|
Генератор тумана Haze 500 FT Pro [4]
|
|
Статический диммерный прибор Combi 25 PC [5]
|
Статический диммерный прожектор PAR 64 Short [6]
|
|
Профильный прожектор ETC Source Four 750 [7]
|
Динамический прибор Robe Color Spot 1200 АТ [8]
|
|
Динамический прибор Robe Color Wash 575 AT [9] |
Динамический прибор Robin LEDBeam 150™ [10] |
Методологический этап творческого проекта
Протокол управления приборами художественного освещения
Протокол передачи данных DMX-512 (англ. Digital Multiplex) – это средство управления несколькими (в т.ч. различными по выполняемым функциям) световыми приборами через единый интерфейс. Для передачи данных используется кабель с двумя проводами в общем экране с пятипиновым (иногда с трёхпиновым) разъёмом XLR.
DMX-512 позволяет управлять по одной линии связи одновременно 512-ю (или менее) каналами. Поток данных по протоколу DMX-512 передаётся со скоростью примерно 250 кбит/с в виде последовательности пакетов. Частота обновления пакетов и, соответственно, команд управления световым оборудованием составляет примерно 44 Гц для случая использования всех 512-и каналов. Каждый пакет представляет собой последовательность кадров данных: один кадр содержит значение одного из 512 каналов. Каждый световой прибор имеет определённое количество дистанционно управляемых параметров и занимает соответствующее этим параметрам количество каналов. На каждый канал приходит 8-битный цифровой сигнал, присваивающий регулируемому параметру прибора значение от 0 до 255 (0-100%). Одновременное использование поддерживающих DMX-512 устройств, управляемых с одной консоли, позволяет создавать световые картины и элементы оформления различной степени сложности [1, 11].

Физический смысл протокола DMX-512 [11]
Диммерные приборы не имеют разъёма DMX, поэтому их сетевые провода ведутся в диммерные шкафы, откуда, в свою очередь, сигнал передаётся по DMX-проводу к сплиттеру – усилителю и разветвителю сигнала.
|
Трёхпиновые и пятипиновые DMX-разъёмы [12] |
Пример DMX-сплиттера [12] |
|
|
Схема трёхпинового и пятипинового DMX-терминатора
|
|
← Диммерные шкафы (фото К.А. Колумбаевой) |
Рекомендуется, чтобы длина линии для передачи данных по протоколу DMX-512 не превышала 300 м. Если же по одной линии передаются данные сразу для нескольких приборов, то предельную длину следует сократить. Как правило, приборы соединяются последовательно (каскадно), и в случае обрыва линии подключенные за точкой обрыва устройства не получат сигнал управления. Поэтому во избежание массового сбоя рекомендуется к одной линии подключать не более 20 осветительных приборов. Для большего парка оборудования следует использовать сплиттеры. Для минимизации интерференции и отражения сигналов рекомендуется завершать каждую линию концевым терминатором – «глухим» штыревым разъёмом с припаянным резистором номиналом 120 Ом [13-14].
Аппаратное и программное обеспечение для управления приборами художественного освещения
Рассмотрим также на примере используемого в художественно-постановочной части Театра Эстрады имени Аркадия Райкина. Профессиональное световое оборудование от производителя MA Lighting является одним из самых передовых. Эта компания с момента своего основания в 1983 году расширилась и стала международным лидером в производстве осветительных консолей с компьютерным управлением и сетевых компонентов [15].
|
Консоль grandMA3 compact XT оснащена двумя большими сенсорными мониторами, имеет возможность управлять восемью потоками DMX, т.е. 4 096-ю каналами световых приборов. Важнейшая особенность всей линейки консолей grandMA – возможность создания личного интерфейса, удобного для конкретного осветителя и для конкретного шоу. |
Консоль GrandMA3 compact XT [16] |
Это делает пульт универсальным: он одинаково удобен для создания концертного шоу, спектакля или проведения масштабного фестиваля. На каждом из двух сенсорных экранов можно создать по 10 рабочих окон с интересующими оператора опциями. Также консоль имеет возможность подключения до четырёх дополнительных экранов. Таким образом, создав заранее все необходимые окна, светооператор получает возможность просматривать любые настройки любых приборов наглядно и так, как ему будет удобнее, в т.ч. прямо во время шоу. Также при создании нового проекта можно использовать ранее сохранённые патчи приборов и записанные окна с пресетами. Все версии проектов сохраняются на внутренней памяти пульта.

Примеры выставления рабочих окон на экранах консоли (фото К.А. Колумбаевой):
A – окно отслеживания порядка световых картин спектакля; B – окно расположения групп приборов, световых эффектов и др. команд; С – окно отображения интенсивности диммерных приборов; D – окно схематического расположения приборов в пространстве
|
ПО grandMA onPC – это не только компьютерная эмуляция всей консоли grandMA для обработки и редактирования данных шоу, но и также возможность управления до 4 096 каналами световых приборов. ПО доступно для бесплатного скачивания на ноутбук или планшет на официальном сайте компании MA Lighting. |
ПО grandMA2 onPC на ноутбуке [17] |
Функциональность, а также дисплей grandMA onPC – точно такие же, как на всех консолях grandMA, поэтому у пользователя нет необходимости привыкать к новому интерфейсу ПО. Используемое совместно с ПО для визуализации grandMA 3D (о нём – далее), grandMA onPC становится полноценной дизайнерской студией, которая обеспечивает эффективное предварительное программирование полных световых шоу без использования реальной консоли.
ПО-визуализатор MA 3D позволяет легко проектировать и настраивать любую сцену или макет декораций с помощью средств 2D-рисования и библиотеки основных графических элементов. Можно открыть несколько окон, как в 2D, так и в 3D с любым углом обзора, и они будут обновляться в реальном времени. Все элементы сцены могут быть расположены в направлениях x / y / z и поворачиваться вокруг различных осей. Текстуры для дизайна поверхностей этих элементов можно выбрать из встроенной библиотеки с возможностью добавления собственных графических файлов. Параметры положения и поворота объектов и камер на виртуальной сцене можно контролировать по протоколу DMX. Виртуальное световое оборудование можно свободно перемещать в трёхмерном пространстве через подключенную консоль grandMA2 [18].

Контроль положения прибора художественного освещения (скриншот из grandMA 3D)
Важно помнить, что для получения правильного изображения всех параметров приборов понадобится длительный подготовительный этап, включающий в себя точные расчёты положений всех приборов, составление макета помещения с учётом возможных засветок и отражений света от различных поверхностей (интерьера, декораций и т.д.). Лишь тогда можно создать дизайн-проект светового шоу. Для комфортной и продуктивной работы в данной программе необходим достаточно мощный ПК, как для работы с графикой или анимацией.

Пример визуализации в ПО grandMA 3D (скриншот из программы)
Устройства беспроводной радиопередачи сигнала управления
по протоколу DMX-512
Подавляющее число светооператоров всё ещё предпочитают проводную связь, а сценических площадок с применением беспроводных технологий крайне мало. Беспроводное радиоуправление световым оборудованием обладает рядом достоинств, которые не могут быть обеспечены традиционным проводным управлением. Это высокая мобильность светового оборудования даже во время сценических действий (при наличии аккумуляторов), облегчение монтажа/демонтажа при создании площадки или обновлении парка оборудования. Однако высокая вероятность ошибок вследствие наложения радиопомех от других устройств беспроводной связи (мобильных телефонов) и существенные задержки передачи радиосигнала управления из-за наличия репитеров для его усиления являются решающим недостатком, объясняющим низкую распространённость использования беспроводной передачи. Сегодня данный способ используется только на небольших временных выставках, на некоторых малых сценических площадках и иногда на ивент-шоу.
Важно отметить, что задержка реакции световых приборов на отправленную команду является особенно важным показателем в световом оформлении музыкальных постановок, где зачастую световые переходы по художественной задумке должны совпадать с музыкальной долей, акцентами или обрывом фонограммы. Задержка более чем на 0,3 секунды, будет заметна зрителю, секундную и более длительную задержку уже можно считать грубой ошибкой.
Существующие устройства беспроводной радиопередачи DMX-сигнала состоят из DMX-разъёмов (чаще всего 3-пин XLR), передающей антенны и схемы на основе микроконтроллера. Работают они в некоммерческой радиочастотной полосе от 2.4 ГГц до 2.525 ГГц (в полосе ISM − Industrial-Scientific-Medical) [19, 20].
Устройства беспроводной радиопередачи сигнала по протоколу DMX
от компании ООО «Энжи» (передатчик и приёмник) [19 20]
Для преобразования цифрового сигнала в большинстве беспроводных DMX-приёмопередатчиках используется GFSK-модуляция (Gaussian Frequency-Shift Keying) – вид частотной манипуляции, при которой значения символов информационной последовательности отображаются путем скачкообразного изменения частоты несущего колебания.
Для более эффективного использования частотной полосы также применяется технология FHSS (Frequency Hopping Spread Spectrum) − метод обработки сигнала с целью расширения его спектра. Согласно этому методу, частотный диапазон разбивается на полосы шириной 1 МГц, называемые RF-каналами. Данные передаются по одному RF-каналу, но сам канал изменяется псевдослучайным образом − в соответствии с числовой последовательностью, известной устройству-отправителю и устройству-получателю. Для построения сигнала используется частотно-временная матрица, каждый столбец которой отображает временную позицию, а строчки соответствуют условному номеру RF-канала. Данный метод повышает помехозащищённость беспроводной локальной сети, но обладает низкой скоростью передачи данных [21].
Устройства беспроводной оптической передачи сигнала
Беспроводная оптическая связь осуществляется посредством технологии АОЛС (атмосферные оптические линии связи) – вид оптической связи, передающей информационный сигнал через атмосферу в виде электромагнитных волн оптического диапазона. Для осуществления такой связи необходимо обеспечить прямую видимость между излучателем и приёмником и специальные атмосферные оптические системы. В качестве источника в настоящее время используют лазер [22]. Связь устанавливается посредством соединения «точка-точка». Информация поступает на приёмопередающий модуль, на котором она кодируется и модулируется. Лазер, установленный в передатчике, передаёт информационный сигнал в виде модулированного оптического излучения инфракрасного диапазона (0,82 мкм), которое фокусируется оптической системой в узкий коллимированный луч и передаётся через атмосферу на приёмник. Приёмником является высокочувствительный фотодиод, преобразующий световой сигнал в электрический [23]. Т.к. в оптическом диапазоне практически отсутствует проблема электромагнитной совместимости и ограничения на ширину спектра сигнала, то применяется прямое преобразование электрического цифрового сигнала в оптический.
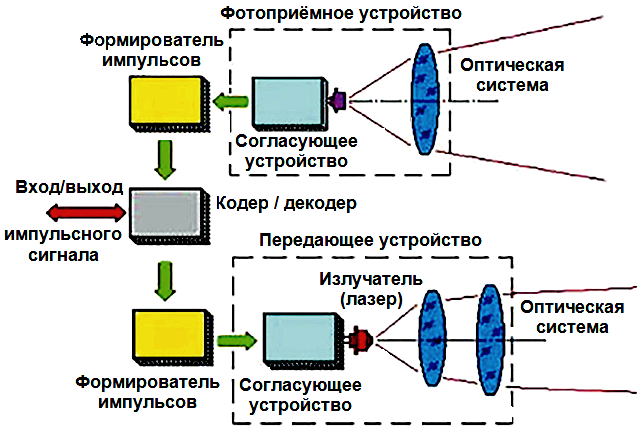
Структурная схема модуля приёма/передачи АОЛС [24]
Преимуществом использования АОЛС является отсутствие необходимости в лицензировании частотного диапазона и отсутствие создания помех для радиоэлектронного оборудования. Недостатками являются: во-первых, необходимость в наличии системы наведения между излучателем и приёмником для обеспечения бесперебойной работы, и, во-вторых, уязвимость АОЛС к погодным условиям, затрудняющим прямую видимость.
Российская компания ЗАО «Мостком» [25], основанная в 2001 году специалистами Научно-исследовательского института газоразрядных приборов, проектирует и поставляет ряд моделей устройств АОЛС. Компания предоставляет потребителям АОЛС-терминалы для стационарных объектов и для объектов, работающих в космическом пространстве (на дистанциях 5000÷50000 м), также ведутся разработки моделей для мобильных (автомобили, самолёты, БПЛА, корабли и т.д.) объектов и для работы под водой. Стационарные терминалы Artolink обеспечивают беспроводную связь на расстоянии от 50 до 7000 м со скоростью передачи до 1 Гбит/с. При этом обеспечивается лёгкий процесс первоначального наведения и автоматическая калибровка под заданную дистанцию.
В состав любой модели Artolink входят два идентичных поста, каждый из которых состоит из приёмопередающего модуля (ППМ), устройства внешнего интерфейса и соединительного кабеля внутреннего интерфейса. Пара ППМ образуют атмосферный оптический тракт. Оптико-механическая система ППМ позволяет регулировать волновой фронт лазерного излучения, снижая его нестабильность, и эффективно отделять оптический сигнал от посторонних засветок, в том числе солнечного света.
Поскольку фактор погодных условий сведён к минимуму для зрелищных мероприятий в закрытых помещениях и может быть проконтролирован для открытых концертных площадок, представляется целесообразным использовать именно АОЛС в тракте передачи сигналов управления световым оборудованием, и в частности, оборудование Artolink.
Модернизация системы управления художественным освещением
В рамках работы над проектом инженером отдела световой аппаратуры Театра Эстрады им. А. Райкина К.А. Колумбаевой были произведены расчёты и замеры, позволившие определить оптимальное размещение осветительных приборов, а также устройств формирования и передачи команд управления (в частности, приёмника и передатчика АОЛС) [26]. Рационально поместить приёмник АОЛС и, соответственно, DMX-радиопередатчик, в самой высокой точке по центру, над зеркалом сцены. В рамках технологий управления световыми приборами несколько потоков, передающих DMX-сигнал, могут быть мультиплексированы и конвертированы в сетевой протокол Art-Net посредством устройства ArtGate [27].
Пример внешнего вида устройства ArtGate [27]
Для создания оптической линии связи от консоли управления световым оборудованием до точки расположения приёмника АОЛС целесообразно выбрать устройство Artolink M1-10GE [28].
Внешний вид Artolink M1-10GE [28]
В модель Artolink M1-10GE встроена система автонаведения, позволяющая быстро и точно наводить приёмопередающие модули друг на друга в процессе первичной установки и поддерживать положение оптической оси при дальнейшей эксплуатации. Для данной модели характерна повышенная надёжность связи за счёт увеличения длины волны основного информационного канала (1550 нм вместо 785 нм).
Выполнение оптического передатчика в виде источника с низкой пространственной, но высокой временной когерентностью, повышает устойчивость связи в неоднородном оптическом канале. Также в модели предусмотрена технология двойного канала, то есть помимо основного может быть организован резервный канал связи с автоматическим переключением между ними [25, 28].
Для последующей передачи команд управления в виде радиосигналов могут быть использованы любые современные DMX-приёмопередатчики, например, SMART-DMX-Transmitter (передатчик) и SMART-DMX-Receiver (приёмник) российской компании Arlight [29].
Устройства беспроводной передачи:
SMART-DMX-Transmitter (слева) и SMART-DMX-Receiver (справа) [29]
При этом надёжность и помехоустойчивость связи будет выше в сравнении с традиционной радиочастотной передачей команд управления за счёт уменьшения площади участка радиопередачи. Важно отметить, что предложенная система беспроводного управления исключает увеличение задержки, которая бы имела место в случае использования только радиочастотной передачи и применения репитеров для усиления сигнала.
Более подробно вопрос модернизации системы для беспроводного управления приборами художественного освещения с обоснованием её структуры и конкретными предложениями по размещению светового оборудования рассмотрен в совместной статье Колумбаевой К.А. и Перелыгина С.В. [26], которую можно скачать по ссылке
Информация о временном творческом коллективе:
Перелыгин С.В., к.т.н., доцент кафедры АВСиТ ГИКиТ СПб;
Гудинов К.К., ст. преподаватель кафедры АВСиТ ГИКиТ СПб;
Башарин С.А., профессор кафедры АВСиТ ГИКиТ СПб;
Пестриков В.М., профессор кафедры АВСиТ ГИКиТ СПб;
Тихонова Л.С., доцент кафедры АВСиТ ГИКиТ СПб;
Куклин С.В., к.т.н., профессор, преподаватель высшей категории КВТК ГИКиТ СПб;
Колумбаева К.А., инженер отдела световой аппаратуры СПбГБУК «Театр Эстрады им. А.И. Райкина»
Библиографический список:
1. Келлер М. Этот фантастический свет. Искусство и проектирование сценического освещения. – М.: 2008. – 224 С.
2. Мельник А. В. Театрально-концертное постановочное освещение: основы постановочного видео. – [Электронный ресурс] // URL: https://lightsoundnews.ru/a-melnik-teatralno-kontsertnoe-postanovochnoe-osveshhenie-osnovy-postanovochnogo-video (Дата обращения: 8.01.2024)
3. FAZE 1050 FT™ | Products | ROBE Lighting [Электронный ресурс] URL: https://www.robe.ru/faze-1050-ft (Дата обращения 22.02.2024)
4. HAZE 500 FT Pro™ | Products | ROBE Lighting [Электронный ресурс] URL: https://www.robe.ru/haze-500-ft-pro (Дата обращения 22.02.2024)
5. Combi 25 PC прожектор c линзой РС 4°- 66° [Электронный ресурс] URL: https://www.lightingpro.ru/catalog/svetovoe-oborudovanie/theatrical-lighting/com-25-pc-spotlight.html?ysclid=ltvucogvm6926659044 (Дата обращения 22.02.2024)
6. Парблайзеры (PAR): Прожектор DTS PAR 64 CLASSIC SHORT Электронный ресурс] URL: http://www.show-light.ru/svetovoe-oborudovanie/svetovoe-oborudovanie-lamps/parblajzery-par/prozhektor-dts-par-64-classic-short-detail (Дата обращения 22.02.2024)
7. ETC Source Four 750 [Электронный ресурс] URL: https://sistema-stage.ru/catalog/stsenicheskiy_svet/profilnye_prozhektory/etc_source_four/ (Дата обращения 22.02.2024)
8. ColorSpot 1200 AT ™ | Products | ROBE Lighting [Электронный ресурс] URL: https://www.robe.cz/colorspot-1200-at (Дата обращения 22.02.2024)
9. ColorWash 575 AT Zoom™ | Products | ROBE Lighting [Электронный ресурс] URL: https://www.robe.cz/colorwash-575-at-zoom (Дата обращения 22.02.2024)
10. LEDBeam 150™ | Products | ROBE Lighting [Электронный ресурс] URL: https://www.robe.ru/ledbeam-150 (Дата обращения 22.02.2024)
11. DMX512 Протокол [DMX-512.RU] [Электронный ресурс] // URL: https://dmx-512.ru/wiki/dmx_512 (Дата обращения: 13.03.2024)
12. Stairville DMX Splitter 4 MK3 19" – [Электронный ресурс] // URL: https://audiobe.ru/muzykalnyj-gipermarket/stairville-dmx-splitter-4-mk3-19-detail.html (Дата обращения: 21.03.2024)
13. DMX Сплиттер (Splitter) разветлитель сигнала DMX [Электронный ресурс] // URL: https://dmx-512.ru/wiki/dmx_splitter (Дата обращения: 19.03.2024)
14. DMX Terminator – [Электронный ресурс] // URL: https://dmx-512.ru/zheleznaja_chast/dmx_terminator?ysclid=luzm6qlts9701814832 (Дата обращения: 19.03.2024)
15. About us | MA Lighting Internetional GmbH [Электронный ресурс] // URL: https://www.malighting.com/company/about-us/ (Дата обращения: 13.04.2024)
16. grandMA3 compact XT | MA Lighting Internetional GmbH [Электронный ресурс] // URL: https://www.malighting.com/product/grandma3-compact-xt-4010505/ (Дата обращения: 15.04.2024)
17. grandma2 – Давид Мисакян [Электронный ресурс] // URL: https://misakyan.com/files/grandma2-setup_2.jpg (Дата обращения: 17.04.2024)
18. MA 3D | MA Lighting Internetional GmbH [Электронный ресурс] // URL: https://www.malighting.com/product-archive/product/ma-3d-grandMA_3D/ (Дата обращения: 18.05.2024)
19. Anzhee Wi-DMX Transmitter Compact – [Электронный ресурс] // URL: https://anzhee.ru/product/anzhee-wi-dmx-transmitter-compact/ (Дата обращения: 13.09.2024)
20. Anzhee Wi-DMX Receiver Compact – [Электронный ресурс] // URL: https://anzhee.ru/product/anzhee-wi-dmx-receiver-compact/ (Дата обращения: 13.09.2024)
21. FHSS - Методы и технологии обработки сигнала - Особенности функционирования беспроводных сетей – [Электронный ресурс] // URL: http://it-servis.ru/dokum/lan/wlan_metod_fhss.php (Дата обращения: 21.09.2024)
22. Атмосферные оптические линии связи. Free Space Optics (FSO) технологии – [Электронный ресурс] // URL: http://www.infinecom.com/ru/solution/ (Дата обращения: 13.10.2024)
23. Беспроводная оптическая связь – [Электронный ресурс] // URL: http://laser-portal.ru/content_568 (Дата обращения: 13.10.2024)
24. FSO технология и её история – [Электронный ресурс] // URL: http://old.moctkom.ru/fsotech.htm (Дата обращения: 13.10.2024)
25. Мостком – Официальный сайт предприятия [Электронный ресурс] // URL: https://moctkom.ru/ru/main_moctkom/ (Дата обращения: 13.10.2024)
26. Колумбаева К.А., Перелыгин С.В. Модернизация системы беспроводной передачи сигналов управления по протоколу DMX‑512 // Актуальные проблемы радио- и кинотехнологий: материалы VIII Межд. науч.-техн. конф. (Санкт-Петербург, 21–22 ноября 2023 г.). – СПб.: СПбГИКиТ, 2024. – С. 32–40.
27. DMX splitter. Сплиттер DMX-512 разветвитель сигналов с поддержкой RDM. – [Электронный ресурс] // URL: https://sunelec.ru/catalog/converters/artgate-pro/ (Дата обращения: 05.11.2024)
28. Стационарные терминалы – Мостком – [Электронный ресурс] // URL: http://www.moctkom.ru/ru/стационарные-терминалы/# (Дата обращения: 7.11.2024)
29. Официальный сайт компании Arlight. – [Электронный ресурс] // URL: https://arlight.su/ (Дата обращения: 05.11.2024)
Творческий проект в медиасфере:
«СИСТЕМЫ УПРАВЛЕНИЯ ХУДОЖЕСТВЕННЫМ
ОСВЕЩЕНИЕМ ТЕАТРАЛЬНОГО ЗАЛА» (продолжение, 2025 г.)
Аннотация:
Светодиодные источники света находят широкое применение в театре и кино и вытесняют тепловые источники. По экономическим и экологическим соображениям целесообразна модернизация существующих осветительных приборов, как альтернатива замены их полностью новыми. Преподаватели КВТК и ГИКиТ СПб кафедр аудиовизуальных систем и технологий и кинооператорского искусства исследуют возможности модернизации театральных прожекторов с целью улучшения показателей эффективности их светооптических систем, влияющих на формирование светового пучка и светоотдачу прибора в целом. Модернизированный светодиодный источник света планируется использовать в существующих осветительных приборах с патроном, рассчитанным на галогенные лампы накаливания.
Методологический этап творческого проекта
Типы светооптических систем театральных прожекторов
Прожектор – осветительный прибор дальнего действия, в котором световой поток источника света перераспределяется и концентрируется оптической системой в направленный пучок света. По виду светооптической системы все прожекторы можно разделить на безлинзовые, однолинзовые и профильные [1].
Светооптическая система безлинзового прожектора состоит из источника света и параболического отражателя. В некоторых приборах также используется сферический контротражатель. Элементы скомпонованы таким образом, что светящееся тело (вольфрамовая нить накала лампы) располагается в фокусе параболического отражателя и одновременно в центре контротражателя, если он присутствует в схеме. Классическим представителем безлинзовых прожекторов является прожектор типа PAR с лампой-фарой. Основным недостатком прожекторов с лампой-фарой является невозможность регулировки ширины луча [2].
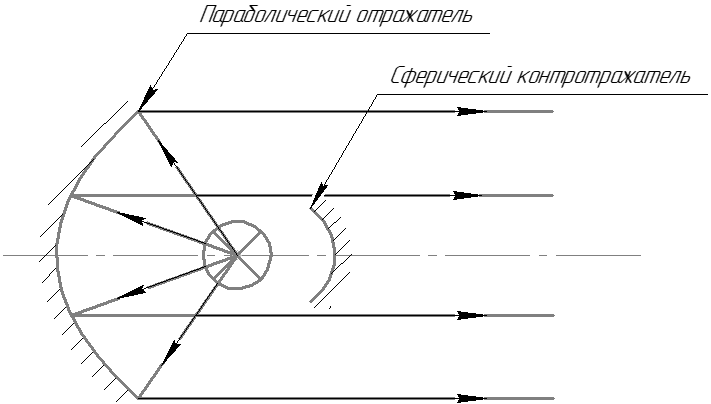

Светооптическая схемабезлинзового прожектора Прожектор типа PAR
Светооптическая система однолинзового прожектора состоит из источника света, сферического отражателя и линзы, выполняющей функции объектива. Источник света расположен в центре сферического отражателя. Световой поток, отразившись от сферы, возвращается по обратному ходу лучей в объём тела накала, формируя изображение спиральных витков между самими витками. Благодаря этому, используется весь световой поток: половина от самого источника в прямом ходе лучей и половина от изображения источника в обратном ходе лучей. Изменять расстояние между источником света и линзой можно либо перемещением линзы, либо перемещением каретки с источником света и отражателем.
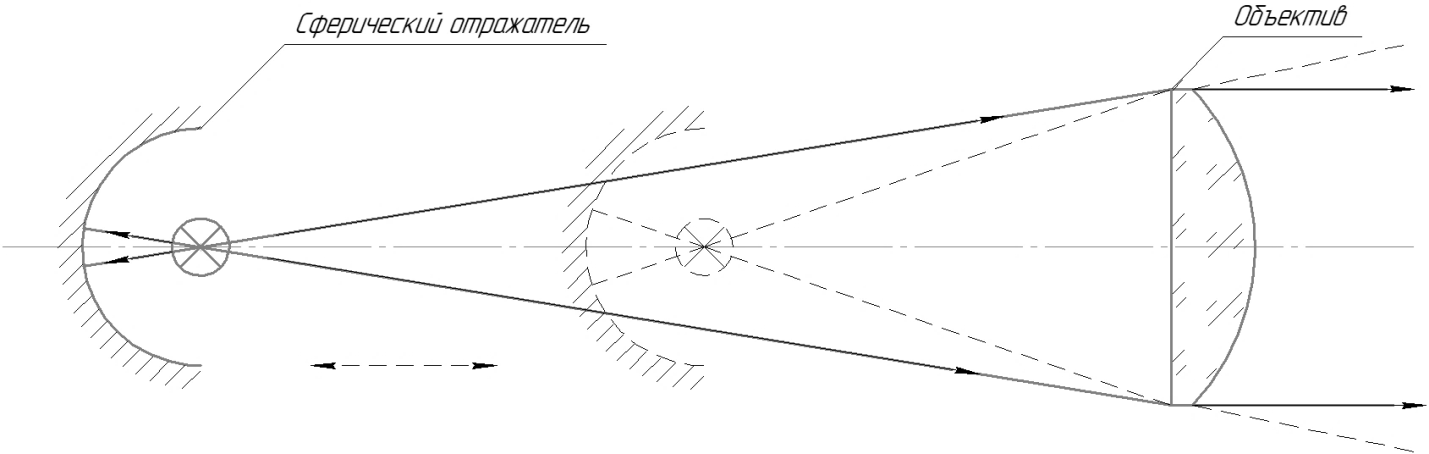
Светооптическая схема однолинзового прожектора

Однолинзовый прожектор с плоско-выпуклой линзой
Профильные прожекторы позволяют формировать луч с заданным профилем. В таких прожекторах изображение формируется в фокальной плоскости оптической системы прожектора с помощью лезвиеобразных заслонок, ирисовой диафрагмы, металлических гобо-трафаретов, стеклянных пластин с фотоизображением [2].

Набор гобо-трафаретов [3]

Примеры луча с заданным профилем [4]
По виду применяемых оптических компонентов профильные прожекторы делятся на эллипсоидные и конденсорные. Структура эллипсоидного профильного прожектора содержит источник света в ближнем фокусе F1 эллипсоидного отражателя. После отражения световой поток собирается в дальнем фокусе F2 эллипса, совпадающем с передним фокусом объектива. Угол раскрытия луча постоянный и определяется фокусным расстоянием объектива.
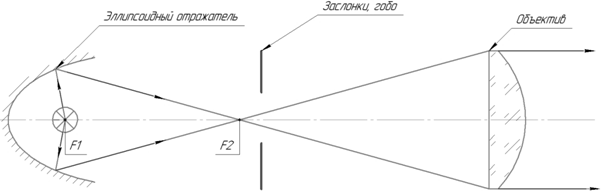
Светооптическая схема эллипсоидного профильного прожектора.

Эллипсоидный профильный прожектор ETC Source Four [5]
В конденсорном прожекторе используется не эллипсоидный, а сферический отражатель и непосредственно линза-конденсор, цель которой – концентрация светового потока и равномерное распределение освещённости поля изображения. Конденсорные прожекторы обычно выигрывают у эллипсоидных аналогов по равномерности освещённости. Однако наличие дополнительной линзы создаёт заметные потери светового потока.
Показатели эффективности светооптических систем
Коэффициент использования светового потока (КПД оптической системы светового прибора) – это отношение светового потока, выходящего из светового прибора, к световому потоку источника света [6]. В идеальном случае весь световой поток источника света направляется оптической системой прожектора к освещаемому объекту. В реальности же это не так, потому как даже при полностью герметичном корпусе и отсутствии «утечки» светового потока через зазоры между деталями, световой поток будет поглощаться элементами конструкции прожектора (корпусом, отражателями, линзами).
Доля светового потока, прошедшего через оптическую систему, определяется коэффициентом пропускания оптической системы по формуле [6]:
τ=(1-ρi)N1*(1-ρпр)N2 *(1-α)l∑*ρ3N3,
ρi– коэффициент отражения от преломляющей непросветлённой поверхности;
ρпр– коэффициент отражения от преломляющей просветлённой поверхности;
α – коэффициент поглощения стекла;
ρ3 – коэффициент отражения зеркальной поверхности;
N1 – число преломляющих непросветлённых поверхностей;
N2 – число преломляющих просветлённых поверхностей;
N3 – число зеркальных поверхностей;
l∑ – суммарная толщина стекла.
Наиболее наглядным примером конструкторского решения, направленного на увеличение коэффициента использования светового потока, является применение контротражателя или использование вытянутых корпусов приборов [2].
| Светораспределение прожекторов и светильников определяется формой фотометрического тела светового прибора и описывается кривыми силы света (КСС). Фотометрическое тело светового прибора представляет собой геометрическое место концов радиус-векторов, выходящих из светового центра прибора, длина которых пропорциональна силе света прибора в соответствующем направлении [7]. |
Фотометрическое тело и КСС |
Кривая силы света (КСС) – это кривая, получаемая сечением фотометрического тела плоскостью, проходящей через оптическую ось светового прибора. Примеры КСС приведены на рисунке [8].
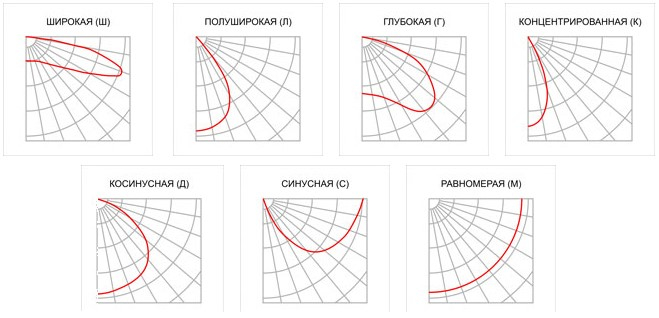
Основные типы КСС
Виды источников света театральных прожекторов
В настоящее время в театральной осветительной технике применяются следующие виды источников света:
· галогенные лампы накаливания
· металлогалогенные газоразрядные лампы
· светодиоды
Галогенные лампы накаливания представляют собой дальнейшее развитие классических вольфрамовых ламп накаливания и обладают значительно большей светоотдачей и сроком службы. Название их обеспечено протекающим внутри колбы лампы циклическим процессом с участием галогенов [9]. Конструктивно галогенные лампы, применяемые в сценическом освещении, разделяются на три типа: с протяжённым телом накала, с концентрированным телом накала, лампы-фары.

Галогенная лампа с протяженным телом накала [10]
 |
 |
| Галогенная лампа-фара PAR-56 [11] | Галогенная лампа с концентрированным телом накала [12] |
Металлогалогенные лампы представляют собой дуговые газоразрядные лампы. В кварцевую колбу такой лампы впаяны два вольфрамовых электрода и вводится, помимо смеси ксенона и аргона, небольшое количество ртути, а также йодида ртути, натрия, лития, таллия, индия и избыточного йода [13]. Спектральные линии свечения используемых металлов и йода находятся в видимой части спектра. Этим обусловлена высокая (до 90 лм/Вт) световая отдача и индекс цветопередачи 85-90 единиц. Лампам также свойственны серьезные недостатки, среди которых: высокая температура колбы (до 1000° С), присутствие в спектре ультрафиолетового излучения, возможность взрыва лампы из-за чрезмерного нагревания, длительное время разжигания и высокое напряжение, требуемое для розжига лампы, невозможность розжига из горячего состояния.
Металлогалогенные лампы находят применение в различных профильных прожекторах, в особенности в приборах типа moving spot и прожекторах следящего света.

Двухцокольная металлогалогенная лампа [14]

Одноцокольная металлогалогенная лампа [15]
Светодиоды – это полупроводниковые источники света, излучающие за счёт происходящей в p-n переходе рекомбинации электронно-дырочных пар. Главными достоинствами светодиодов является их компактность, высокая эффективность и продолжительный срок службы. Излучение светодиодов приходится на узкую часть спектра и является практически монохроматическим.
Большой интерес представляет получение источников белого света на основе светодиодов. Можно выделить две группы светодиодов белого свечения: использующие аддитивное смешение цветов светодиодов и использующие люминофоры. В первом случае традиционно используются RGB-светодиоды, помещённые в один корпус. Однако рост числа светодиодов разного типа часто ведёт к снижению световой отдачи [16]. Во втором случае используются синие светодиоды на основе нитрида галлия, покрытые слоем люминофора, свечение которого приходится на жёлто-оранжевую часть спектра [17]. Таким светодиодам свойственна высокая световая отдача, но низкая цветопередача, обусловленная смешением только двух цветов. Лучших значений цветопередачи (90-93) можно добиться, используя дополнительные слои люминофора.
В настоящее время полихромные светодиодные системы применяются, в первую очередь, в осветительных приборах с возможностью управления цветом излучения.
Информация о временном творческом коллективе:
Перелыгин С.В., к.т.н., доцент кафедры АВСиТ ГИКиТ СПб;
Башарин С.А., д.т.н., профессор кафедры АВСиТ ГИКиТ СПб;
Бурундукова Е.С., преподаватель КВТК ГИКиТ СПб;
Гудинов К.К., ст. преподаватель кафедры АВСиТ ГИКиТ СПб;
Куклин С.В., к.т.н., профессор, преподаватель первой категории КВТК ГИКиТ СПб;
Патрикеева Е.Ю., старший преподаватель кафедры кинооператорского искусства ГИКиТ СПб;
Пестриков В.М., д.т.н., профессор кафедры АВСиТ ГИКиТ СПб;
Тихонова Л.С., к.т.н., доцент кафедры АВСиТ ГИКиТ СПб.
Библиографический список:
1. Демчев В. И., Царьков В. М. Прожекторное освещение, изд. 2e, перераб. и доп. – М., «Энергия», 1972. 80 с., ил.
2. Исмагилов Д. Г., Древалёва Е. П. Театральное освещение: – М. ЗАО «ДОКА Центр», 2014, 456 с.
3. Dedolight Gobo Kit – Set of 6, URL: https://www.bhphotovideo.com/c/product/300822-REG/Dedolight_GOBOKIT_Gobo_Kit_Set.html (дата обращения: 20.01.2025)
4. Световой прибор CHAUVET-DJ LFS-5D. URL: https://www.1music.kz/product/svetovoy-pribor-chauvet-dj-lfs-5d/?ysclid=m6nyxzf54o10378666 (дата обращения: 20.01.2025)
5. Source Four., URL: https://www.etcconnect.com/Products/Lighting-Fixtures/Source-Four/?LangType=1049 (дата обращения: 10.01.2025)
6. Мешков В.В. Основы светотехники: Учеб пособие для вузов. Ч. 1. – 2.е изд., перераб. – М.: Энергия, 1979. – 368 с.
7. Справочная книга по светотехнике/ Под ред. Ю.Б. Айзенберга, 4-е изд. перераб. и доп. М.: Знак 2019. – 972 с.
8. Выбор диаграмм освещенности. URL: https://tatled.ru/articles/vybor-diagramm-osveschennosti.html (дата обращения: 24.02.2025)
9. Афанасьева Е. И., Скобелев В. М. Источники света и пускорегулирующая аппаратура: Учебник для техникумов. – 2-е изд., перераб. – М.: Энергоатомиздат, 1986. – 272 с.
10. OSRAM 64751 1250 W 240 V. URL: https://proflampa.ru/catalog/foto_kinooptika/galogennye_1/dvukhtsokolnye_2/lampa_osram_64751_1250w_240v_r7s/?ysclid=m8ngerx9k4286317781 (дата обращения: 10.03.2025)
11. SYLVANIA PAR 56 300W 12V. URL: https://www.smartlamps.ru/products/sylvania-par-56-300w-12v-klemmy-vintovye-lampa (дата обращения: 10.03.2025)
12. Галогенная лампа GE Lighting T19 1000 W, GX9,5. URL: https://krasnoyarsk.dj-store.ru/oborudovanie/svetovaya_apparatura/lampy-dlya-svetovogo-oborudovaniya/galogennye-lampy/24433_ge-lighting-t19-1000-w-gx95.html (дата обращения: 10.03.2025)
13. Ишанин. Г. Г., Козлов М. Г., Томский К. А. Основы светотехники. – СПб.: Береста, 2004. – 292 с.
14. OSRAM HMI 575/GS 95V/575W SFc-10 1000h. URL: https://www.dj-checkpoint.de/osram-hmi-575-gs-95v-575w-sfc-10-1000h.html (дата обращения: 15.03.2025)
15. PHILIPS MSR 1200 G-22. URL: https://proflampa.ru/catalog/foto_kinooptika/metallogalogennye_1/odnotsokolnye_4/lampa_philips_msr_1200_g22_/?ysclid=m8nh4gfb2591863983 (дата обращения: 15.03.2025)
16. Шуберт Ф. Светодиоды / Пер. с англ. под ред. А.Э. Юновича. – 2-е изд. – М.: ФИЗМАТЛИТ, 2008. – 496 с.
17. Ганская Е. С., Кожокару Д. В., Туев В. И. Влияние толщины и концентрации люминофорной композиции на световую отдачу и коррелированную цветовую температуру светодиода белого цвета свечения // Актуальные проблемы современной науки: материалы VIII Региональной научно-практической конференции с международным участием. – Омск: ОмГТУ. – 2019. – С. 77-80.
Творческий проект «Проекты технологического суверенитета и технологии цифрового прорыва» (2024-2025 гг.)
Проект создания отечественного мультипарадигменного кроссплатформенного языка программирования Корсáков
———
Цели проекта:
Создание отечественного языка программирования общего назначения, способного заменить зарубежные программные решения и обеспечить независимость в сфере информационно-коммуникационных технологий.
———
Основные задачи:
- Интеграция разработки различных модулей и программ: обеспечение независимости через создание отечественных решений.
- Высокий уровень защиты цифровых ресурсов: разработка средств с повышенной безопасностью.
- Популяризация программирования: привлечение широкой аудитории и новых разработчиков.
- Упрощённое обучение: облегчённый процесс освоения для привлечения большего числа специалистов в IT-сферу.
- Суверенитет на уровне кода и мышления: сохранение контроля над разработкой и идеологией продукта.
———
Описание языка Корсáков:
Корсáков – это язык общего назначения, сочетающий парадигмы функционального и объектно-ориентированного программирования. В будущем планируется расширение возможностей за счёт модулей для работы с терминалом, сетевыми протоколами (TCP/IP), файловыми системами и другими компонентами.
———
Поддержка и развитие:
Этот проект одновременно является и студенческим, и грантовым: он получил поддержку Фонда содействия инновациям в рамках грантового конкурса «Студенческий стартап». Сейчас он развивается в компании ООО «РУС.ЯЗ».
———
Продукты проекта:
Основной продукт – независимый от иностранных закрытых решений язык программирования, предназначенный для широкого круга пользователей: от энтузиастов до государственных учреждений и образовательных организаций.
———
Лицензирование продуктов
Для некоммерческих проектов используется лицензия GPLv3. Для коммерческого применения или в целях сотрудничества необходимо связаться с разработчиком – компанией ООО «РУС.ЯЗ» (info@корсаков.рус, @korsakov_info) для обсуждения условий использования.
———
Результаты на текущий момент
На данный момент существует прототип на Python (gitverse.ru/rus.yaz/korsakov_python), поддерживающий кириллицу и латиницу, с разнообразными конструкциями. Однако этот синтаксис уже устарел по сравнению с новыми версиями.
Активная работа ведётся над новым компилятором (gitverse.ru/rus.yaz/korsakov), который сейчас транспилирует код на Корсáкове в ассемблерный код (FASM, архитектура x86-64). В дальнейшем планируется расширить возможности компиляции под разные архитектуры и среды выполнения, а также отказаться от промежуточного этапа транспиляции и сразу собирать исполняемые файлы.
———
Публичные презентации
4 апреля 2024 года в рамках Международной конференции «Молодые учёные в обеспечении безопасности» (АНО ДО «Образовательная орбита», ЭкспоТехноСтраж, КВЦ «Экспофорум») была проведена первая публичная презентация проекта, где были освящены основные аспекты разработки языка, а также его идеология и планы развития.
8 февраля 2025 года в рамках ХX конференции «Свободное программное обеспечение в высшей школе» (ООО «Базальт СПО», ИПС им. А.К. Айламазяна РАН, г. Переславль-Залесский) состоялось освящение результатов проекта спустя полгода с момента начала освоения гранта.
———
Соц. сети и медиаресурсы
Сайт проекта — корсаков.рус
Дневник разработки — @korsakov_rus
Аккаунт для связи — @korsakov_info
Информационная почта — info@корсаков.рус
———
Информация о временном творческом коллективе:
Соколов Денис Андреевич, доцент кафедры аудиовизуальных систем и технологий ФГБОУ ВО «Санкт-Петербургский государственный институт кино и телевидения», председатель Совета молодых ученых СПбГИКиТ член Российского общества «Знание» лектор Российского общества «Знание» член экспертного совета Фонда поддержки молодых ученых имени Геннадия Комиссарова
Лукинов Владислав Алексеевич, член Молодежного парламента Государственной Думы Российской Федерации, старший преподавателькафедры аудиовизуальных систем и технологий ФГБОУ ВО «Санкт-Петербургский государственный институт кино и телевидения, Руководитель региональной лаборатории Молодежного Сообщества «ВЫЗОВ» в г. СПб и ЛО лектор Российского общества «Знание»
Межвузовский творческий проект «Научный диалог с нобелевскими лауреатами по физике» (2023 г.)

Аннотация
В январе 2023 г. состоялся библиографический этап межвузовского творческого проекта «НАУЧНЫЙ ДИАЛОГ С НОБЕЛЕВСКИМИ ЛАУРЕАТАМИ ПО ФИЗИКЕ» совместно с кафедрой информационных управляющих систем СПбГУТ им. проф. М.А. Бонч-Бруевича. Представлена презентация аннотированного обзора научного проекта в области квантовой теории и квантовых технологий. Методологической основой научных исследований являются работы нобелевских лауреатов по физике 2022 г.
(А. Аспект (Франция), Д. Клаузер (США), А. Цайлингер (Австрия)), а также работы основоположников квантовой теории, выдающихся ученых XX в.
Новизна и теоретическая значимость проекта
Компьютерные эксперименты по концептуальным аспектам квантовой теории в истории науки, возможно, не проводились, учитывая данные обзора литературы и источников по тематике проекта. В научных исследованиях используются графические иллюстрации симметрии в квантовых корреляциях запутанных фотонов с нарушением неравенства Белла в квантовой теории. В работе применяются методы Монте-Карло и современные системы программирования С++ и Maple.
Библиографический этап творческого проекта
В истории науки хорошо известен почти философский спор двух гигантов, Эйнштейна и Бора, начавшийся публично в 1927 году. Первый утверждал, что "Бог не играет в кости" и вероятностные предсказания квантовой механики, разительно отличающиеся от привычного детерминизма классической физики, лишь свидетельство неполноты теории. Бор же утверждал, что вероятность тут вовсе не случайна, что это закон природы, что так устроен квантовый мир.
Совершенно замечательно то, что затянувшийся спор постепенно удалось привести к экспериментально проверяемым математическим соотношениям. Эти соотношения, неравенства Белла, были написаны физиком-теоретиком Беллом в работе [4] 1964 года, посвящённой анализу знаменитого парадокса Эйнштейна, Подольского, Розена (ЭПР -парадокса) 1935 года, который должен был окончательно убедить Бора и всех его последователей в неполноте квантовой механики [2].
Неравенства Белла выведены в предположениях классической физики. Было показано, что если квантовая теория справедлива, то эти неравенства могут нарушаться (теорема Белла). После этого началась экспериментальная проверка неравенств. Считается, что более убедительным был эксперимент Алена Аспекта [1], проведённый им в 1982 году в лаборатории под Парижем. В эксперименте неравенства Белла нарушались, значит, по крайней мере один из тех "незыблемых" принципов классического детерминизма, на которых опирались неравенства Белла, оказался неверным в применении к микромиру.

Парадоксальные знания квантовой механики в работах нобелевских лауреатов по физике А.Энштейна, Н.Бора, Э.Шредингера: (парадоксы «Кот Шредингера» и «Мышь Эйнштейна».

Эволюция квантовой концепции «корпускулярно-волнового дуализма» в работах нобелевского лауреата по физике, академика Л.Ландау.

Мнение о перспективах квантовой науки, основоположника квантовой электродинамики и квантовой информатики, нобелевского лауреата по физике Р.Фейнмана.

Обзор работ «второй волны» квантовой теории: эксперименты с запутанными фотонами проф. Д. Белла, парадоксы Эйнштейна-Подольского-Розена.
Корреляции между удаленными измерениями для двух раздельных систем, которые перед этим взаимодействовали, обычны для классического мира. Например, если механический объект с нулевой импульсом (или моментом) разделяется на две части в результате некоторого внутреннего фактора, то импульс (момент) каждой отдельной части остается равным и взаимно противоположным во время их дальнейшей свободной эволюции. В общем случае, когда каждый из фрагментов подвергается некоторому взаимодействию, два импульса (момента) остаются коррелированными, поскольку они в каждый момент времени определены их начальными значениями, которые, в свою очередь, имели точно определенную сумму [1].
Можно использовать такую классическую картину, чтобы с ее помощью учесть ЭПР-корреляции, базируясь на общих свойствах двух систем. Кажется возможным «понять» ЭПР-корреляции с помощью такого классического образа, используя разные значения дополнительного параметра для различных пар. Можно надеяться, что статистические предсказания квантовой механики просто усредняют результат по значению дополнительного параметра. Кажется, что такой же была и позиция Эйнштейна. Следует заметить, что на этой стадии рассуждений следование данной позиции не противоречит квантовой механике: не возникает логических проблем, если полностью принять предсказания квантовой механики и привлекать дополнительные параметры, дающие приемлемый образ ЭПР-корреляций. Таким образом, приходим к тому, чтобы рассматривать квантовую механику как описание статистической механики на более глубоком уровне.
Фундаментальная теорема Белла утверждает, что локальные теории с дополнительными параметрами приводят к неравенствам Белла; некоторые предсказания квантовой механики нарушают неравенства Белла и, следовательно, квантовая механика несовместима с локальными теориями с дополнительными параметрами. Неравенство Белла интересно не столько само по себе в его математическом формализме, сколько своим происхождением и глубиной вопросов, для решения которых оно было придумано и использовано.

Библиографический список
1. Aspect А., Bertlmann R., Zeilinger A. From Bell to Quantum information, Quantum speakables, 2002.
2. Einstein А., Podolsky В., Rosen N., Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? // Phys. Rev. — American Physical Society, 1935. — Vol. 47, Iss. 10. — P. 777-780.
3. Фок В.А. Можно ли считать, что квантово-механическое описание физической реальности является полным? // УФН, том XVI, выпуск 4. — 1935. — С. 436—457.
4. Bell J.S. On the Einstein Podolsky Rosen paradox // Physics Vol. 1, No. 3, pp. 198—200, 1964 Physics Publishing Co. Printed in the United States.
5. Манин Ю.И., Вычислимое и невычислимое. М.: Сов. радио, 1980.
6. Парфенов П.С. Квантовая механика. Методическое пособие к практикуму по квантовой физике. — СПб: НИУ ИТМО, 2012. — 133 с.

Методологический этап творческого проекта (2023 г.): моделирование и формализация экспериментов Белла в квантовой оптике
Неравенства Белла в квантовой оптике выводятся из предположения, что у обеих частиц существуют определенные параметры с момента их рождения до поглощения детектором. Рассмотрим двухканальный тест, представленный на рис. 1.
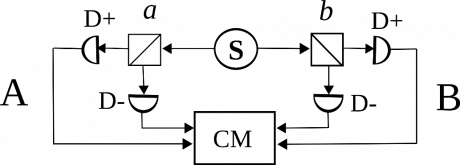
Рис. 1. Схема двухканального теста [1]
Источник S производит пары "фотонов", посылаемых в противоположных направлениях. Каждый фотон сталкивается с двухканальным поляризатором, ориентация которого может быть установлена экспериментатором. Возникающие сигналы из каждого канала обнаруживаются и совпадения подсчитываются CM-монитором совпадений. Неравенство Белла при таком эксперименте выглядит следующим образом: ![]() .
.
В данном уравнении a и a' являются настройками детектора на стороне A, b и b' на стороне B. Выражение для математического ожидания E(a, b) и др. представляют собой квантовые корреляции пар частиц, где квантовая корреляция определяется как ожидаемое значение произведения «результатов» эксперимента, то есть статистическое среднее значение A(a)·B(b), где A и B — отдельные результаты, использующие кодирование +1 для канала '+' и -1 для канала '−'.
Проводятся четыре отдельных эксперимента, соответствующих четырем выражениям E(a, b). Значения a,a ',b ,b ' обычно выбираются на усмотрение проводящего эксперимент, при этом, стараются выбрать те, для которых квантово-механические формулы вероятностей (формально совпадающие с законом Малюса для поляризованного света) дает наибольшее нарушение неравенства [1].
Для каждого выбранного значения a и b записывается количество совпадений в каждой категории. Затем вычисляется экспериментальная оценка для E(a, b). После того, как все E были оценены, можно найти экспериментальную оценку S. Если полученное значение больше 2, неравенство считается нарушенным и эксперимент объявляется подтверждающим предсказание квантовой механики и исключающим все теории локальных скрытых переменных.
Современные научные методы исследований и алгоритмизация в компьютерных экспериментах с квантовой запутанностью (2023 г.)

Квантовая запутанность есть явление, подразумевающее незримую связь между состояниями двух частиц. Изменение квантового состояния одной частицы неминуемо приведёт к изменению другой связанной с ней. Соль ещё и в том, что такое взаимодействие произойдет быстрее скорости света и нарушает принцип локальности.
В статье "The speed of quantum information and the preferred frame: analysis of experimental data и Experimental test of nonlocal quantum correlation in relativistic configurations", опубликованной в 2000-2001 годах, ученые используют простую логику детектирования. Расположив две запутанные квантовые частицы в специальных устройствах, они проводят одновременные измерения квантовых состояний этих частиц. Детектирование проводится одним и тем же световым пучком, который разделяется на два контура. Изменение состояния одной частицы мгновенно (или, как минимум, быстрее скорости света), вызывает изменение состояния и другой частицы. Через несколько лет подобный эксперимент был проведен снова, и методика была усовершенствована увеличением времени измерений.
В 2015 году журнал Nature опубликовал статью научного коллектива, который фактически ещё раз доказал существование квантовой запутанности на практике. Причём, чуть ли не впервые было обозначено, что запутанность может существовать на расстоянии, измеряемом световыми годами! Эксперимент продолжался 18 дней и количество итераций составило не менее 250. Исследователи облучали одинаковым потоком энергии два алмаза, расположенные на расстоянии 1,3 км друг от друга, что заставляло алмазы испускать фотоны. Фотоны взаимодействовали друг с другом посредством оптического кабеля. В результате испустившие их электроны в алмазах запутывались, а их квантовая функция стала одинаковой.
Есть и практические применения эффекта квантовой запутанности. Так, в 2019 году было заявлено, что сотрудники МФТИ смогли реализовать работающий прототип квантового компьютера. Именно квантовая запутанность там является движущей силой для кубитов. Но если вам и эта информация покажется неубедительной (к сожалению, есть основания не доверять громким высказываниям...Детали раскрывать не буду, но кое-кто говорил, что сделал работающую машину времени), то давайте посмотрим на зарубежные публикации. Например, в этой статье в журнале Nature, описывается методика работы квантового процессора и приведены результаты реальных экспериментов.
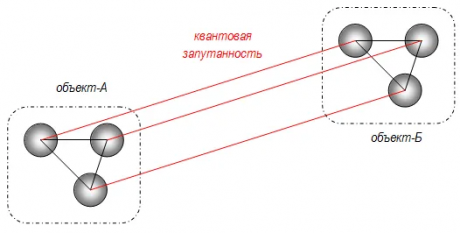

Джон Стюарт Белл (1928-1990, Северная Ирландия), доктор философии по физике (1956). Член Лондонского королевского общества (1972). Почётный член Американской академии искусств и наук (1987). Медаль Дирака от Института физики (1988). Медаль Хьюза (1989). Премия Хайнемана (1989). В 2009 году Центр квантовой информации и квантового контроля (англ. Centre for Quantum Information & Quantum Control) Университета Торонто учредил премию Джона Стюарта Белла.
В квантовых экспериментах Белла с запутанными фотонами процесс измерений интенсивности поляризованного света удается формализовать с помощью алгоритмов теории вероятностей и математической статистики, рассматривая поляризационные квантовые числа для состояний фотонов дискретными случайными величинами в четырехмерном пространстве элементарных событий для четырех поляризаторов с разными углами плоскости поляризации (a, a', b, b'), т.е. для законов распределения поляризаций фотонов в четырех лучах (A, A', B, B') можно записать матрицы с определяемыми вероятностями:
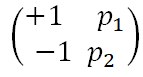 .
.
Предполагая, что интенсивность света с запутанными фотонами пропорциональна вероятностям состояний поляризации частиц и закон Малюса для поляризованного света можно получить формулы вероятностей, аналогичные квантово-механическим решениям в формализме волновых функций. Заметим, что независимость событий обеспечивается наносекундным временем физических измерений в лаборатории. В силу симметрии двухканального теста (рис.1) и нормировки вероятностей в пространстве элементарных событий для вероятностей состояний фотонов для двух поляризаторов можно записать:
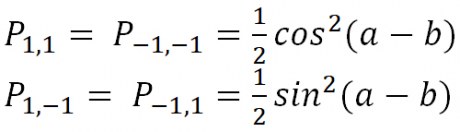

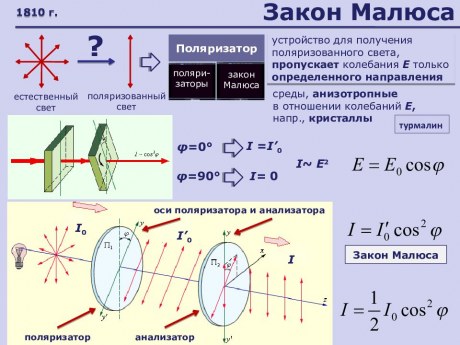
Этьенн Луи Малюс (1775-1812, Париж, Франция)
В 1810 году создал теорию двойного лучепреломления света в кристаллах. Открыл закон, впоследствии названный его именем, об интенсивности линейно поляризованного света, прошедшего через поляризатор. Предложил способ определения направления оптической оси кристалла.
Для определения математических ожиданий случайных величин, входящих в неравенство Белла, сопоставим разным комбинациям состояния поляризации фотонов (1,1),(-1,-1),(1,-1),(-1,1) величину вида AB c распределением:
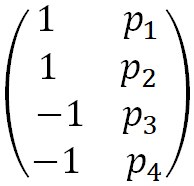
Математические ожидания подобных случайных величин можно определить аналитическим методом (по формулам) и исследовать неравенство Белла с помощью компьютерной графики. В этом случае, данный алгоритм позволяет разработать и исследовать компьютерно-аналитическую модель эксперимента с квантовой запутанностью. Если вероятности и средние вычисляются с помощью генерации случайных чисел на компьютере, то предложенный вероятностно-статистический метод (метод Монте-Карло) позволяет исследовать численную модель квантового эксперимента. При этом необходимо определить алгоритм выбора состояний поляризации фотонов, учитывая оптический закон Малюса. В этом случае вероятности состояний (или площади на рис.2.) приобретают зависимость от квадрата косинуса угла плоскости поляризатора, т.е. в программе реализации алгоритма возможен условный оператор, например, в цикле Maple:
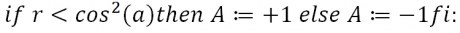
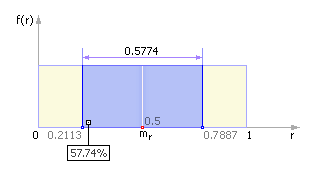
Рис.2 Равномерная плотность распределения стандартного генератора случайных чисел
В физическом эксперименте нельзя уверенно предсказать, какое возможное значение примет каждая из случайных величин, но можно предвидеть, какое значение примет их среднее арифметическое. Теорема Чебышева справедлива не только для дискретных, но и для непрерывных случайных величин.
Обычно для измерения некоторой физической величины производят несколько измерений и их среднее арифметическое принимают в качестве искомого. К физическим величинам можно применить теорему Чебышева, если: 1) они попарно независимы, 2) имеют одно и то же математическое ожидание, 3) дисперсии их равномерно ограничены.
Первое требование выполняется, если результат каждого измерения не зависит от результатов остальных. Второе требование выполняется, если измерения произведены без систематических (одного знака) ошибок. В этом случае математические ожидания всех случайных величин одинаковы. Третье требование выполняется, если прибор обеспечивает определенную точность измерений. Хотя при этом результаты отдельных измерений различны, но рассеяние их ограничено.
Если все указанные требования выполнены, мы вправе применить к результатам измерений теорему Чебышева: при достаточно большом n вероятность неравенства 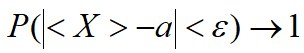 .
.
Другими словами, при достаточно большом числе измерений, почти достоверно, что их среднее арифметическое как угодно мало отличается от истинного значения измеряемой величины.
Итак, теорема Чебышева указывает условия, при которых описанный способ измерения может быть применен. Однако ошибочно думать, что, увеличивая число измерений, можно достичь сколь угодно большой точности. Дело в том, что сам прибор (методика эксперимента) дает показания с конечной точностью, ограничивающей точность эксперимента.
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А равна р. Можно ли предвидеть, какова примерно будет относительная частота появлений события? Положительный ответ на этот вопрос дает теорема, доказанная Якобом Бернулли (опубликована в 1713 г.), которая получила название «закона больших чисел» и положила начало теории вероятностей как науке. Доказательство Бернулли было сложным; простое доказательство дано П.Л. Чебышевым в 1846 г. Итак, теорема Бернулли утверждает, что сходится по вероятности 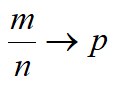 при
при 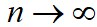 . Из данных соображений выбирается число измерений в квантовом эксперименте (или квантовое число, определяющее интенсивность света).
. Из данных соображений выбирается число измерений в квантовом эксперименте (или квантовое число, определяющее интенсивность света).
Императивное программирование в компьютерном эксперименте на языке С++ и Maple

История и перспективы С++
Первые ЭВМ программировались непосредственно в машинных кодах. Написание, чтение и изменение кода программ, состоящего из чисел, было затруднительно, поэтому появились т. н. языки ассемблера — запись машинных кодов в виде слов. Код на языке ассемблера по структуре не отличался существенно от машинного, кроме того, что был проще для восприятия человеком. Из-за этого перенос программ между ЭВМ оказывался затруднителен, если у них были разные системы команд. Одновременно код оставался невыразительным с точки зрения логики программы. Преодолеть эту проблему удалось путем создания первых высокоуровневых языков программирования (Fortran, COBOL, LISP, BASIC), однако они еще более жестко опирались на платформу (систему кодов) ЭВМ, для которой реализовывались, и не для каждой платформы выпускался компилятор (в силу сложности языков). В 1972 году инженерами компании Bell Labs Брайаном Керниганом (Brian Kernighan) и Дэннисом Ритчи (Dennis Ritchie) были опубликованы первые версии языка С для машин PDP-11. В его основу были заложены принципы:
а) Высокий уровень, то есть использование конструкций, отражающих логику программы (циклы, ветвления, подпрограммы), а не порядок выполнения машинных кодов (сравнения, переходы).
б) Гибкость и мощность, сиречь возможность на С сделать не менее функциональную программу, чем на чистом ассемблере (пользуясь возможностью вставлять в программу на С части ассемблерного кода).
в) Простота компиляции и независимость от платформы, призванная максимально упростить создание компиляторов С под новые ЭВМ. В язык не вносилось тех средств, которые можно было бы реализовать на нем самом как библиотеки (например, ввод-вывод).
Таким образом, язык С позволял вести разработку любого ПО (будучи «высокоуровневым ассемблером») и удобно для программиста как язык высокого уровня (ЯВУ), а перенос программ на другие платформы был предельно упрощен — достаточно было реализовать сравнительно простой компилятор. Будучи создан с учетом нужд практики, язык С быстро завоевал всемирную популярность. Реализации языка С зачастую немного отличались, поэтому в 1989 году ANSI установил стандарт на язык С — ANSI C89, чтобы зафиксировать элементы языка и состав 5 стандартной библиотеки.
Следующий аналогичный стандарт, самый популярный, появился через 10 лет: ANSI C99, а в 2011 году — его обновление, стандарт C11.1.2 Язык С++. Язык С имел процедурную парадигму, то есть предполагалось структурирование кода при помощи подпрограмм (функций и процедур). К началу 80-х выяснилось, что для создания сложных приложений этого недостаточно. Среди предложенных удачных решений было объектно-ориентированное программирование (ООП). Его встроенная поддержка отсутствовала в С, поэтому, начиная с 1984 года, Бьярн Страуструп из Bell Labs разрабатывал новый язык программирования на основе C с поддержкой ООП, в конечном счете названный С++. Самым привлекательным свойством С++ стала забота об обратной совместимости (backward compatibility) с C и собственными предыдущими версиями.
Разработчики зачастую могли использовать большое количество готового кода прямо в программах на новом языке и быть уверенными, что его не понадобится переписывать. Очевидная выгода от этого способствовала почти столь же широкому распространению С++, как и С. В ходе развития язык С++ претерпевал изменения и многочисленные эксперименты, иногда спорные, но большинство из них оставалось в языке.
Одновременно появлялись другие языки, основанные на ООП: Objective-C (совместим с С), Java, Object Pascal (Delphi), C#, где многие ошибки проектирования С++ были учтены и не повторялись. Они оказались удачны для новых приложений, однако во многих случаях переписывать с С++ имеющийся код было нецелесообразно, либо новый код активно использовал старый на С++, либо требовалась одновременно производительность и кроссплатформенность. Таким образом, язык С++, в некотором смысле, «проложил дорогу» многим последующим языкам, иногда более удобным.
В настоящее время С++ используется для создания высокопроизводительных, кроссплатформенных или низкоуровневых приложений и библиотек. Это связано с тем, что данные приложения имеют сложную структуру и нуждаются в высокоуровневых средствах языка (ООП), но в то же время требуется возможность низкоуровневых операций (работа с памятью, ассемблерные вставки) и большая производительность (за счет контроля использования ресурсов). Также С++ используется при поддержке старого, или унаследованного, кода (legacy code).
Области применения:
- Графика. Во-первых, это визуализация в технических приложениях, например, при расчетах конструкций, в медицине, физике. Во-вторых, это индустрия развлечений — кинематограф и видеоигры (для игровых приставок альтернатив С++ зачастую нет).
- Математические расчеты. Дело в том, что современные компиляторы имеют хорошие средства оптимизации на уровне машинного кода, в частности, код может автоматически быть приспособлен для многопроцессорного параллельного исполнения. Диалекты С и С++ применяются в технологиях CUDA и OpenCL — для высокопроизводительных вычислений на векторных процессорах (например, на видеокартах).
- Высокопроизводительные системы, действующие в условиях ограниченных ресурсов машины и жестких требований по скорости работы. Это системы управления базами данных (СУБД), web-серверы, обработка звука и видео, особенно потоковая и в реальном времени.
- Системное и низкоуровневое программирование. Во-первых, это ядра операционных систем и драйверы устройств, во-вторых, на С и С++ часто программируются специальные устройства (микроконтроллеры, платы, сетевое оборудование).
- Крупные прикладные библиотеки (frameworks), например, библиотеки пользовательского интерфейса — MFC, Qt, wxWidgets, Gtk+, виртуальные машины и интерпретаторы языков программирования.
- Кроссплатформенные программы, в которых требуется что-либо из вышеперечисленного.
Фрагмент кода программы на С++
#include
#include
#include
#include
using namespace std;
int main() {
srand(time(0));//определение начального времени
//определение переменных
int m, n;
// n, m – квантовые числа
//создание динамического двумерного массива на m строк
float ** arr = new float*[m];
/*создание каждого одномерного массива в динамическом двумерном массиве, или иначе - создание столбцов размерности n*/
for (int i(0); i < m; i++)
arr[i] = new float[n];
//заполнение массива
{ }
//расчет математических ожиданий A'B и AB'
//итоговый расчет и вывод значений
S=AB+A1B-AB1+A1B1;
}
return 0;
}
Программирование и построение линии тренда в системе символьной математики Maple
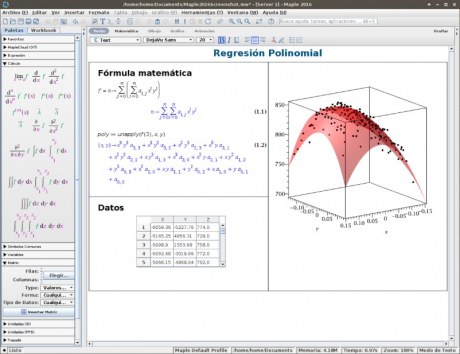
Фрагмент кода программы в среде Maple:
restart: with(plots): with(Optimization): #with(stats): # Модули программы nf:=100: m:=3:alfa:=0: beta:=0: beta1:=45: alfa:=evalf(convert(alfa degrees,radians)):beta:=evalf(convert(beta degrees,radians)): beta1:=evalf(convert(beta1 degrees,radians)): # Глобальные переменные SQM:=evalf(2*sqrt(2)); Sexp:=2.70;
#Процедура Bell Bell := proc(alfa1) #type(x,'matrix'(float));
local s1,s2,s3,s4,r,ab,a1b1,ab1,a1b,Scomp,gam,gam1,X,a1,i; #Локальные переменные
global j,n; #x:=Matrix(n,4): # массивы
Sb := Bell(22.5); h := .5; num := 720; Num := num; alfa1 := 0; for j to num do Sbell[j] := Bell(alfa1); y[j] := Sbell[j]; angle[j] := alfa1; x[j] := angle[j]; alfa1 := alfa1+h end do; P := [seq([x[j], y[j]], j = 1 .. num)];
pointplot(P, style = line, numpoints = 800, color = black); arg[1] := 1; arg[2] := 2; arg[3] := 3; s[1] := 2.828; s[2] := 2.70; s[3] := 2.45; arg[1] := s[1]; arg[2] := s[2]; arg[3] := s[3]; p := [seq([arg[j], s[j]], j = 1 .. 3)];
pointplot(p, style = point*numpoints and point*numpoints = 800, color = black)
N := Num; xc := 22.5; xc := evalf(convert(xc*degrees, radians));
f := proc (x) options operator, arrow; sqrt(2)*cos((1/180)*a*(x-xc)*Pi+b)+1 end proc; S := proc (a, b) options operator, arrow; sum((y[n]-f(x[n]))^2, n = 1 .. N) end proc;
res := NLPSolve(S(a, b), {a >= 0, b >= 0}, assume = nonnegative); p := map(op, 2, res); q := map2(op, 2, p); a := q[1]; b := q[2]; r1 := sum((y[n]-f(x[n]))^2, n = 1 .. N); ysr := (sum(y[n], n = 1 .. N))/N; r2 := sum((y[n]-ysr)^2, n = 1 .. N); R2 := 1-r1/r2; plot(f(x), x = 0 .. 360, y = -.5 .. 2.5);
#Графическое решение и линия тренда
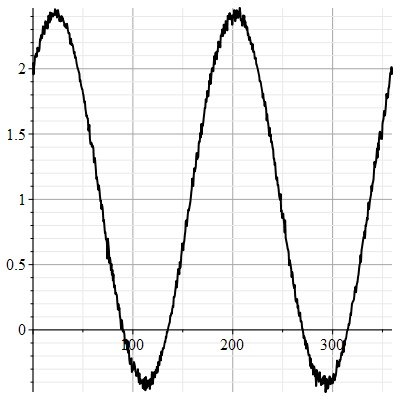
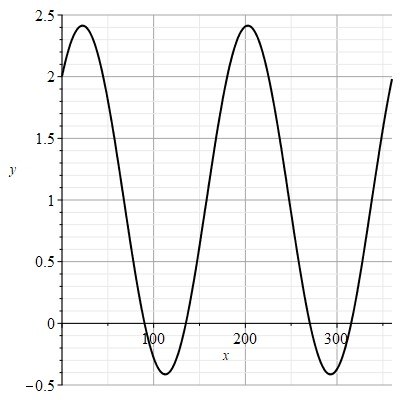
Апробация и достоверность научных результатов


Творческий проект в медиасфере
«Устройства пространственной обработки акустических сигналов
в медиаиндустрии»
Библиографический этап творческого проекта (2023 г.):
Системы с двумя микрофонами способны улучшить отношение сигнал/помеха (ОСП) речевого сигнала (РС) целевого диктора в присутствии широкополосной помехи или речи стороннего диктора. Одним из способов является применение адаптивного компенсатора помех (АКП) [1, 2, 3]. Эффективность АКП зависит от геометрии размещения микрофонов. Наиболее распространенным является размещение микрофона опорного канала вблизи источника помехи. Однако если источником помехи является сторонний диктор, микрофон опорного канала не всегда удается разместить вблизи него. В этом случае эффективность АКП может быть ограничена попаданием речи целевого диктора в опорный канал компенсатора [1].
Методологический этап творческого проекта (2023 г.):
Модель акустической сцены
На рис.1 представлена схема акустической сцены с целевым диктором и источником помех.
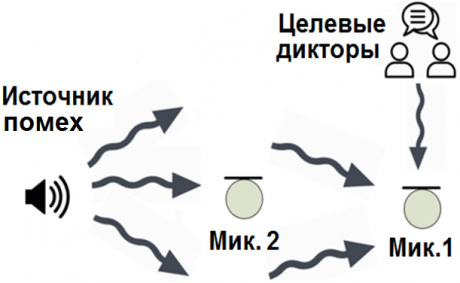
Рис. 1. Схема акустической сцены
Допустим, что интенсивность источников сигнала и помехи одинакова, звук от источников к микрофонам распространяется прямолинейно в свободном пространстве. Тогда ОСП в произвольной точке M(x, y), где установлен микрофон, равно [4, 5]:
 ,
,
где  – интенсивности источников сигнала и помехи,
– интенсивности источников сигнала и помехи, 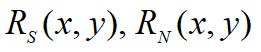 – расстояния от точки М до источников сигнала и помехи соответственно.
– расстояния от точки М до источников сигнала и помехи соответственно.
На рис. 2 показаны изолинии ОСП в разных точках планарной акустической сцены. Вблизи источника целевого сигнала ОСП максимально, вблизи источника помехи – минимально.
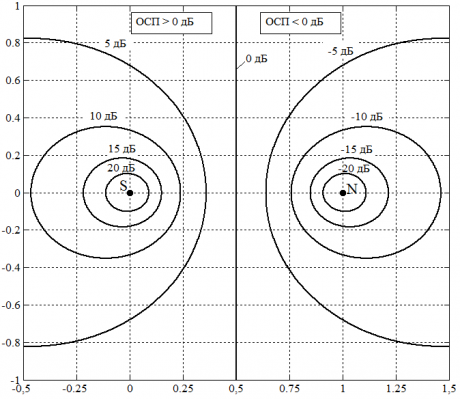
Рис. 2. Изолинии постоянного ОСП
Компенсация помехи с использованием АКП
АКП позволяет частично компенсировать помеху и тем самым увеличить ОСП целевого сигнала. На рис. 3 представлена схема АКП с микрофонами М1 основного канала и М2 опорного канала [1].
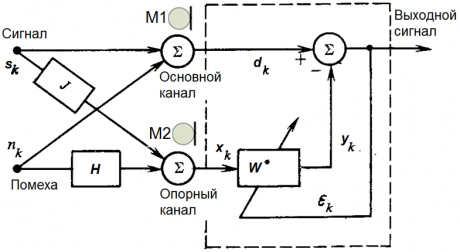
Рис. 3. Схема АКП с двумя микрофонами
Обозначим сигналы микрофонов символами X1, X2. Считаем, что микрофон М1 принимает неискаженный целевой речевой сигнал (РС) и неискаженный сигнал помехи, что соответствует равенству единице передаточных функций сигнала и помехи для микрофона М1.
Общая модель сигналов АКП имеет вид:
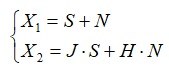 (1)
(1)
где J, H – передаточные функции сигнала и помехи для микрофона М2,
S и N – целевой сигнал и помеха соответственно.
Целевой сигнал и помеха считаются статистически независимыми. Рассмотрим различные сценарии выделения РС.
1) Если передаточные функции J, H известны, то целевой сигнал S можно получить, решив систему уравнений (1). Однако в практических приложениях эти функции неизвестны. Возможным решением этой проблемы является адаптивная оценка этих функций в паузах целевого сигнала или паузах помехи [7]. Частными случаями этой технологии является оценка функции H в паузах целевого сигнала S или оценка функции J в паузах помехи N на основе согласованной фильтрации [3].
Тогда возникают следующие варианты.
2) Если в паузах сигнала S получена оценка функции H, можно вычислить оценку целевого сигнала, которая, однако, будет иметь погрешность:
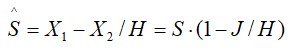
3) Если в паузах помехи получена оценка функции J, можно вычислить преобразованную помеху:
![]()
Информацию о преобразованной помехе можно использовать для адаптивной компенсации помехи в сигнале первого микрофона, минимизируя среднеквадратическую ошибку сигнала:
![]()
где < > - обозначает операцию усреднения по времени.
После настройки фильтр АКП будет иметь передаточную функцию, равную ![]() .
.
Тогда на выходе АКП достигается полная компенсация помехи [1]:
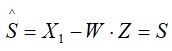
Рассмотрим общий случай согласованной фильтрации сигналов X1 и X2 при использовании сигнала X2 в качестве опорного. Компенсация помехи основана на согласовании фаз и амплитуд помехи в обоих каналах с помощью адаптивно настраиваемого фильтра АКП и вычитании оценки помехи из сигнала основного канала:
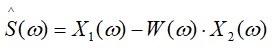
В результате настройки АКП передаточная функция фильтра определяется на основе оценки фильтра Винера [1]:
![]() ,
,
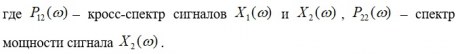
Условие увеличения отношения сигнал/помеха
Поскольку в каждом из каналов (и основном, и опорном) присутствуют сигналы целевого источника и помехи, то АКП настраивается на совместную компенсацию, как помехи, так и целевого сигнала.
В [6] исследованы вопросы расположения микрофонов основного и опорного каналов относительно источников сигнала и помехи для увеличения ОСП основного канала.
На рис. 4. серым цветом выделены области допустимого расположения микрофона М2 при различном расположении М1.
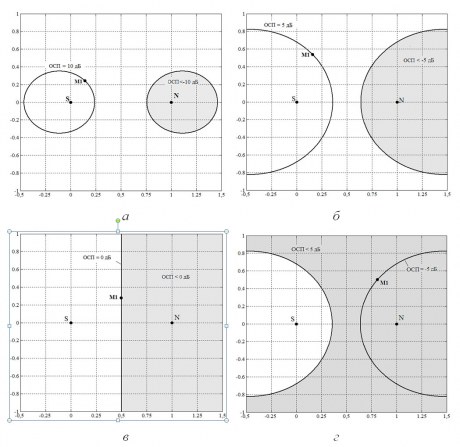
Рис. 4 – Области расположения М2 для различных положений М1:
![]()
Отметим, что область возможного расположения микрофона М2 на рис. 4 (г) определена на основе формальных соотношений. На практике микрофон М2, расположенный в левой половине акустической сцены, целесообразно использовать в качестве микрофона основного канала.
Выводы:
Эффективность выделения речи целевого диктора с помощью АКП зависит от размещения микрофонов основного и опорного каналов. Область допустимого расположения микрофона опорного канала ограничена уровнем интенсивности помехи. В общем случае микрофон опорного канала следует располагать как можно ближе к источнику помехи, а микрофон основного канала как можно ближе к источнику целевого сигнала. В случае, когда расстояние от микрофона опорного канала до источника целевого сигнала меньше расстояния до источника помехи, целесообразно поменять местами микрофоны для основного и опорного каналов. Для уменьшения искажений целевого сигнала целесообразно вести настройку АКП в паузах помехи (на интервалах активности источника целевого сигнала). Перспективным способом преодоления перечисленных проблем является применение двухэлементной микрофонной решетки [8].
Библиографический список:
- Уидроу Б., Стирнз С. Адаптивная обработка сигналов // М.: Радио и связь, 1989. 440 c.
- Bitzer J., Brandt M. Speech Enhancement by Adaptive Noise Cancellation: Problems, Algorithms and Limits // Proc. Int. Conf. AES 39, 2010, pp.106-113.
- Vary P., Martin R. Digital Speech Transmission: Enhancement, Coding and Error Concealment // Wiley, 2006, 644 P.
- Акустика: учебник для ВУЗов / Ш.Я. Вахитов и др., под ред. проф. Ю.А. Ковалгина. – М.: Горячая линия – Телеком, 2009. – 660 с.
- Ковалгин Ю.А., Вологдин Э.И. Аудиотехника. Учебник для вузов — М.: Горячая линия – Телеком, 2013. – 742 с.
- Столбов М.Б., Перелыгин С.В. Двухмикрофонный адаптивный компенсатор помех: особенности построения // Актуальные вопросы развития индустрии кино и телевидения в современной России: материалы IV Нац. науч.-практ. конф. (Санкт-Петербург, 18–20 окт. 2021 г.). – СПб.: СПбГИКиТ, 2021. – С. 20-24
- Compernolle D.V. Switching adaptive fifilters for enhancing noisy and reverberant speech from microphone array recording // In: Proc. IEEE Internat. Conf. on Acoust., Speech, Signal Processing, 1990, Vol. 1, pp. 833-836.
- Столбов М.Б., Перелыгин С.В. Алгоритмы двухэлементной микрофонной решетки для выделения речевых сигналов в присутствии когерентных помех // Цифровая обработка сигналов. 2017. №4. С. 34-39
Информация о временном творческом коллективе:
Перелыгин С.В., к.т.н., доцент кафедры АВСиТ ГИКиТ СПб
Гудинов К.К., ст. преподаватель кафедры АВСиТ ГИКиТ СПб
Мальцева В.А., к.ф-м.н, доцент кафедры АВСиТ ГИКиТ СПб
Столбов М.Б., к.т.н., доцент ФИТиП НИУ "ИТМО"
«Метод контроля состояния цифровых носителей информации»
Проект рассматривает вопросы сохранности архивных записей. Представлены критерии оценки качества и состояния цифровых носителей и корректирующие возможностей помехоустойчивых кодов. Описан метод контроля состояния цифровых носителей, учитывающий особенности появления повреждений на носителях в процессе их хранения. Спроектировано устройство диагностики компакт-дисков, реализующее разработанный метод, даны рекомендации по его использованию
Комплекс программ «Анимационная модель вращательного броуновского движения»
В научном проекте кафедры аудиовизуальных систем и технологий СПбГИКиТ, посвященном фундаментальным исследованиям в термодинамике и молекулярно-кинетической теории рассматриваются методологические аспекты реализации модели научного исследования в системе технического образования. Основой создания теории физического явления является феноменологический подход, создающий общую картину явления и устанавливающий основные фундаментальные соотношения без подробной детализации модельных представлений, на основе использования фундаментальных научных законов и надежно установленных экспериментальных данных.
Комплекс программ «Анимационная модель вращательного броуновского движения» завершает цикл научных исследований кафедры аудиовизуальных систем и технологий в области современной методологии стохастического моделирования реальных процессов и систем.
В ходе научных исследований вращательной броуновской динамики:
- проведены исследования в теории чисел, приведены компьютерные иллюстрации гипотетического нормального свойства фундаментальных констант в десятичной и двоичной системе счисления;
- разработан табличный генератор псевдослучайных чисел с равномерным распределением (π-генератор), проведен статистический тест программы. Получен явный вид плотности распределения χ2-критерия и графическая интерпретация статистического критерия в системе компьютерной алгебры Maple;
- разработана компьютерная модель случайных блужданий в поступательном броуновском движении, а также анимационная модель исторического опыта Капплера во вращательной броуновской динамике в рамках вероятностно-статистического подхода с использованием π-генератора псевдослучайных чисел, классической плотности вероятности осциллятора и функций системы символьной математики.
Для разработки анимационной модели определены критерии выбора компьютерной среды, языка программирования и библиотек:
- возможность реализации модели на выбранном уровне детализации;
- простота освоения доступных команд библиотек языка и компиляции полученного кода;
- материальная доступность, наличие бесплатной лицензии на программное обеспечение;
- опыт работы исследователя в выбранной среде, уровень знакомства с синтаксисом языка, парадигмами программирования и доступными библиотеками;
- способность работы языка на платформах Windows и Linux (кроссплатформенность).
Высокий уровень языка Python помогает быстро осваивать его особенности и не заботиться о множественных сложностях языков низкого уровня. Широкое распространение языка предоставляет возможность выбирать инструменты построения графики и анимации из множества доступных библиотек. Библиотека PyPI (The Python Package Index) содержит более сотни тысяч различных проектов. Широкое сообщество пользователей позволяет получить поддержку при возможном возникновении проблем. Свободная лицензия Python Software Foundation License позволяет использовать язык без каких-либо ограничений. Кроссплатформенность позволяет разрабатывать приложения в операционной системе Linux с рабочего ноутбука, при необходимости имея возможность перейти на другую известную платформу.

Скриншоты программы анимационного моделирования вращательного броуновского движения
Для визуализации опыта используется набор инструментов для графики и анимации. Стандартом для платформонезависимой прорисовки графики является OpenGL – спецификация двух- и трёхмерной графики. OpenGL также не зависит от языка программирования и имеет привязки к множеству из них, в том числе к Python. Одной из python-библиотек, работающих с OpenGL, является Pyglet. Pyglet позволяет рисовать OpenGL примитивы, работать с окном, управлять временем для создания анимации, загружать мультимедиа-объекты.
Разработанная компьютерная программа используется для исследования дифференциальных уравнений динамической модели вращательного броуновского движения, в которой рассматриваются малые колебания в окрестности положения равновесия крутильного маятника.

Перспективы практического использования программы «Анимационная модель вращательного броуновского движения», правообладателем которой является СПбГИКиТ, связаны с актуальными проблемами проектирования интеллектуальных систем математического моделирования реальных процессов и систем, а также с методикой их изучения. Полученные результаты применимы в новых методических разработках в области моделирования и формализации, специальность 05.13.18- Математическое моделирование, численные методы и комплексы программ, а также в образовательных программах направлений подготовки 11.03.01- Радиотехника, 44.03.01- Педагогическое образование, модуль- Информатика, информационные технологии и вычислительная физика, 09.03.02- Информационные системы и технологии.
Проекты кафедры прошлых лет:
«Разработка методов реставрации фонограмм на основе авторегрессионной модели»
Проведены исследования эффективности удаления щелчков и шума из фонограммы методом авторегрессивного моделирования звуковых сигналов. Разработан алгоритм реставрации фонограммы, осуществляющий процедуры обнаружения поврежденного участка и восстановления сигнала на этом участке. Получены программы в среде Матлаб, позволяющие устранить щелчки и фоновый шум из фонограммы
«Исследование троичных цифровых устройств обработки сигналов»
Научно-исследовательская работа посвящена исследованию цифровых устройств, использующих троичную алгебру логики. Практическим итогом работы является синтез, реализация и функциональное моделирование в среде Simulink различных троичных устройств, осуществляющих обработку
аудиовизуальных сигналов с учётом сниженной потребляемой мощности и
высокого быстродействия
«Разработка метода автоматического выделения монтажных планов на основе анализа гистограмм видеоряда»
Выполнен обзор существующих в настоящее время методов обнаружения монтажных стыков. Изучен инструментарий, необходимый для разработки программного обеспечения. Исследованы признаки видеоряда кинофильмов, по которым производится автоматическое обнаружение монтажных стыков. Разработаны алгоритмы выделения монтажных планов, дана оценка их эффективности
«Разработка формантного фильтра для электромузыкальных инструментов»
В работе проведены исследования современных музыкальных стилей, направлений и применение в них частотной обработки музыкального звукового сигнала. Разработаны метод формантной фильтрации и теоретическая модель формантного фильтра электрогитары на основе речевого аппарата человека. Проведены лабораторные испытания эффективности модели формантного фильтра электрогитары с привлечением фокус-группы. Разработан формантный фильтр электрогитары
«Исследование цифрового частотного детектора на основе преобразователя Гильберта»
В проекте рассматривались вопросы исследования методов минимизации нелинейных искажений в схемах детектирования ЧМ-сигналов посредством перевода данных схем на цифровую реализацию. Рассматривалась история развития ЧМ-систем, приводится обзор существующих принципов построения ЧМ-детекторов. Описан метод реализации детектора радиосигналов с частотной модуляцией, реализованный на основе преобразования Гильберта. Представлены рекомендации к реализации аппаратной части цифрового частотного детектора
КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ ВОЛНОВЫХ ПРОЦЕССОВ
В АКУСТИКЕ ТВЕРДОГО ТЕЛА
Актуальность исследования заключается в изучении современных компьютерных технологий вычислений в задачах математического моделирования нелинейных динамических систем с дискретной трансляционной симметрией в контексте решения фундаментальной проблемы Ферми-Паста-Улама (ФПУ) о применимости законов термодинамики и статистической физики к системам ФПУ. Рассматриваются методические аспекты изучения фундаментальных научных проблем и достижений современных компьютерных технологий.
Новизна
Впервые в практике медиаобразования показана возможность изучения классических парадоксов вычислительной физики и физики твердого тела в современном компьютерном эксперименте. Дана статистическая интерпретация закона равномерного распределения энергии по степеням свободы в результатах численного моделирования цепочки нелинейных связанных осцилляторов Ферми-Паста-Улама. Апробирована методика расчета энергии длинных наноразмерных акустических цепочек. Приведены результаты вычислительного эксперимента со статистической обработкой данных:
- исследован механизм волнового процесса в акустической цепочке с определением скорости распространения уединенной волны методами регрессионного анализа;
- проведен спектральный анализ нелинейных колебаний в многомерном фазовом пространстве с использованием алгоритма быстрого преобразования Фурье (FFT). Оптимизация методов программирования с использованием численных методов, функций символьных преобразований в системах компьютерной математики обеспечивает минимальный размер файла программы компьютерного эксперимента, текст которой, может состоять, практически, из нескольких строк, написанных на удобном алгоритмическом языке.
- В частных случаях доказан закон равномерного распределения энергии по степеням свободы в термодинамическом равновесии для длинных наноразмерных акустических цепочек, приведены иллюстрации в интерактивной компьютерной графике;
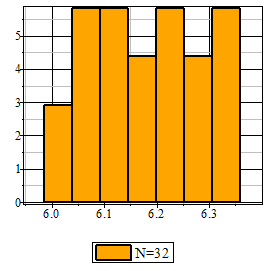
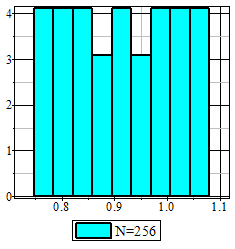
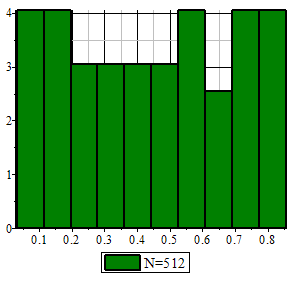
- Разработана методика компьютерного эксперимента в теории алгоритмов. Обнаружены пороговый эффект во временной сложности алгоритмов, а также влияние технологии программирования на класс алгоритмической задачи. Для алгоритма ФПУ построена, практически с единичной достоверностью, линия тренда полиномом четвертой степени в широком диапазоне размера акустических цепочек.
Теоретическая и практическая значимость
В научном проекте развита теория математического и компьютерного моделирования в физической акустике и акустике твердого тела при изучении физических свойств нелинейных динамических систем с трансляционной симметрией в контексте решения фундаментальной проблемы Ферми-Паста-Улама.
В работе использовалось современное программное и математическое обеспечение, интерактивная графика системы компьютерной математики Maple 17 и Excel. Разработаны алгоритмы и комплексы программ математического моделирования нелинейных динамических систем с дискретной симметрией на примере длинных наноразмерных акустических цепочек Ферми-Паста-Улама.
Участник проекта, студентка СПбГИКиТ А.С.Корчагина стала победителем III Международного конкурса научно-методических и выпускных квалификационных работ «ГНОЗИС» 2016 года (н.рук. проф. А.И.Ходанович). В конкурсе, проводимом Международным исследовательским центром «Научное сотрудничество», приняли участие 150 участников из Республики Армения, Республики Беларусь, Республики Казахстан и Российской Федерации, представивших для конкурсного рассмотрения курсовые работы, дипломные, бакалаврские и магистерские проекты, выполненные в 2015/2016 учебном году на базе высших и средних учебных заведений. Отмечается теоретическая и практическая значимость работы для научных направлений 05.13.18- Математическое моделирование, численные методы и комплексы программ, 01.04.06- Акустика (технические науки, физико-математические науки) и направления подготовки бакалавров 11.03.01- Радиотехника.

СОВРЕМЕННЫЕ ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ СТОХАСТИЧЕСКОГО МОДЕЛИРОВАНИЯ В ЗАДАЧАХ ТЕХНИЧЕСКОЙ ФИЗИКИ
Цель и задачи исследования - состоит в разработке методов стохастического моделирования динамических систем с дискретной симметрией и изучение физических свойств системы связанных осцилляторов Ферми-Паста-Улама (ФПУ). Разработка и изучение компьютерных моделей случайных блужданий со случайным шагом, а также экспериментов по вращательной броуновской динамике. Провести анализ научно-методической литературы по теме исследования и на этом основании определить методологию научного исследования в разработке программного обеспечения компьютерных экспериментов с фундаментальными стохастическими моделями технической физики; провести апробацию результатов выпускной квалификационной работы.
Актуальность исследования заключается в изучении современных компьютерных технологий вычислений в задачах стохастического моделирования при изучении фундаментальных проблем технической физики: применимость законов термодинамики и статистической физики к системам ФПУ в термодинамическом пределе, обобщение закона случайных блужданий в случайной среде, а также компьютерное моделирование экспериментов по вращательной броуновской динамике. Рассматриваются методические аспекты изучения фундаментальных научных проблем и достижений современных информационных технологий.
Новизна
Впервые в практике выпускных квалификационных работ показана возможность изучения фундаментальных задач технической физики в современном компьютерном эксперименте. Дана статистическая интерпретация закона равномерного распределения энергии по степеням свободы в результатах численного моделирования цепочки нелинейных связанных осцилляторов Ферми-Паста-Улама со случайными массами. Апробирована методика расчета энергии длинных неоднородных наноразмерных акустических цепочек. Приведены результаты вычислительного эксперимента со статистической обработкой данных:
- в частных случаях доказан закон равномерного распределения энергии по степеням свободы в термодинамическом равновесии для неоднородных длинных наноразмерных акустических цепочек, приведены иллюстрации в интерактивной компьютерной графике. Показано влияние неоднородностей на соотношение средних потенциальной и кинетической энергий. В случае термодинамического равновесия в термодинамическом пределе возможна оценка молярных теплоемкостей системы ФПУ в определенном диапазоне температур;
- разработана методика компьютерного эксперимента в броуновской динамике. Получен закон диффузии в модели одномерных случайных блужданий со случайным шагом, а также разработан алгоритм генерации случайных чисел в случае броуновской вращательной динамики.
Теоретическая и практическая значимость
В выпускной квалификационной работе развита теория математического и компьютерного моделирования при изучении фундаментальных динамических моделей в технической физике.
В работе использовалось современное программное и математическое обеспечение, интерактивная графика системы компьютерной математики Maple 17 и Excel. Разработаны алгоритмы и комплексы программ математического моделирования дискретных динамических систем на примере длинных неоднородных наноразмерных акустических цепочек Ферми-Паста-Улама, случайных блужданий в случайной среде, а также экспериментов по вращательной броуновской динамике.
Разработанный программный продукт целесообразно и возможно использовать в научной работе, при изучении технической и прикладной физики для иллюстраций и демонстрационных примеров в общем курсе физики, а также при изучении дисциплин «Математические методы описания сигналов», «Прикладные математические методы в радиотехнике», «Гармонический анализ» для направления подготовки бакалавров 11.03.01 – Радиотехника, «Информационные технологии», «Технологии программирования» для направления подготовки бакалавров 09.03.02- Информационные системы и технологии.
Результаты научного исследования апробированы на международной и межвузовской научно-практических конференциях, материалы научных статей представлены в печати. В перспективе развития тематики возможно получение новых результатов в научных исследованиях методологии технической физики и информационных технологий моделирования реальных процессов и систем.

ДЕМОНСТРАЦИОННЫЙ ЭКСПЕРИМЕНТ С МАЯТНИКОМ ФУКО
Опыт Фуко – это достижение астрономии и натурфилософии Коперника и Кеплера, Галилея и Ньютона, Кориолиса и самого Фуко; в теоретической физике устанавливает границы применимости законов классической механики в инерциальных системах отсчета, в компьютерном эксперименте- численное моделирование динамических траекторий в неинерциальной системе отсчета.
Совместными усилиями преподавателей и студентом в нашем Институте был создан маятник Фуко, один из самых крупных в Европе (длина нити 27 м, масса 60 кг), позволяющий проводить прецизионные измерения при изучении фундаментальных законов физики.


Оригинальность научного проекта кафедры, посвященного прецизионным измерениям с помощью маятника Фуко, в компьютерном моделировании траектории свободных колебаний, инженерных решениях и экспериментальной реализации опыта на значительно меньшей площадке, чем в музее Тартуского университета (Эстония).
В измерениях ускорения свободного падения с помощью маятника Фуко участвовали студенты гр. 732 Дмитрий Баталов и Екатерина Бурундукова. Для автоматизации измерений ребята использовали видеофиксацию с частотой 240 к/сек, что позволило измерить ускорение свободного падения с высокой точностью (рук. к.п.н., доцент Б. М. Штейн).


По данным социальных сетей всего в мире моделей маятников Фуко несколько десятков, в том числе в США, Франции, Румынии, Австралии, Кувейте и других странах. В основном они устанавливаются только в университетах, научных музеях и планетариях. В штаб-квартире ООН в Нью-Йорке тоже висит маятник Фуко, а самый большой из всех маятников Фуко находится в Конференц-центре Орегон в Портленде, США (27 метров нить и масса 408 кг). Маятник Фуко в СПбГИКиТ один из самых крупных маятников в Европе, позволяющий проводить учебный физический эксперимент с более точными измерениями траектории и ускорения свободного падения, вспоминая историческую фразу Галилея: «И все-таки она вертится!».
Кафедра принимала участие в проекте по лизенцированию направления подготовки бакалавров 072500.62 Дизайн – профиль подготовки «Промышленный дизайн».
Этот проект представлялся интересным для кафедры и для факультета, поскольку в указанном профиле подготовки изучаются технические и творческие дисциплины, вызывающие интерес у абитуриентов и студентов.
Для кинематографа это направление подготовки необходимо с точки зрения возможности компьютерной реализации пространственных декораций и других элементов съемочной площадки.
В области научных исследований кафедра работала над проектом прибора комплексной диагностики кинотеатров по техническому состоянию аппаратуры методами вибрационного, шумового и тепловизионного контроля.
В 2017 году у кафедры был проект по аккредитации направления подготовки 09.03.02 "Информационные технологии".